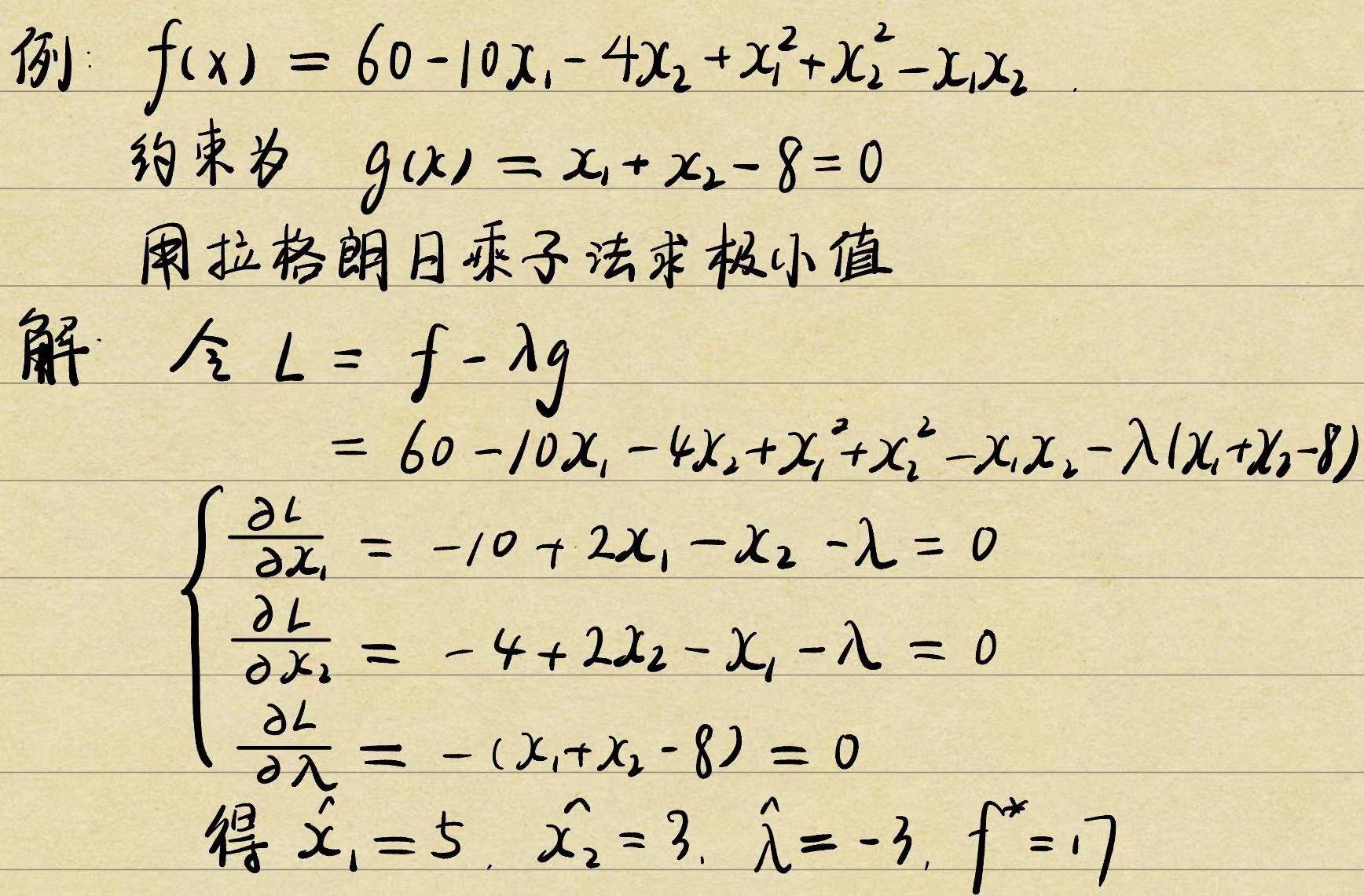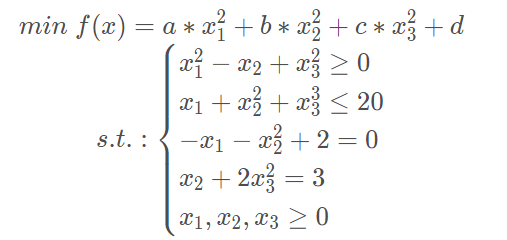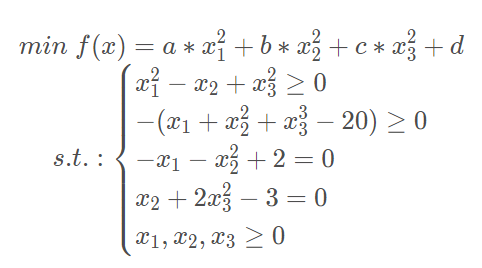最优化理论

Nice

代码实现

写在这里

优化最常用的是，官方文档中说明它包含5个方面：

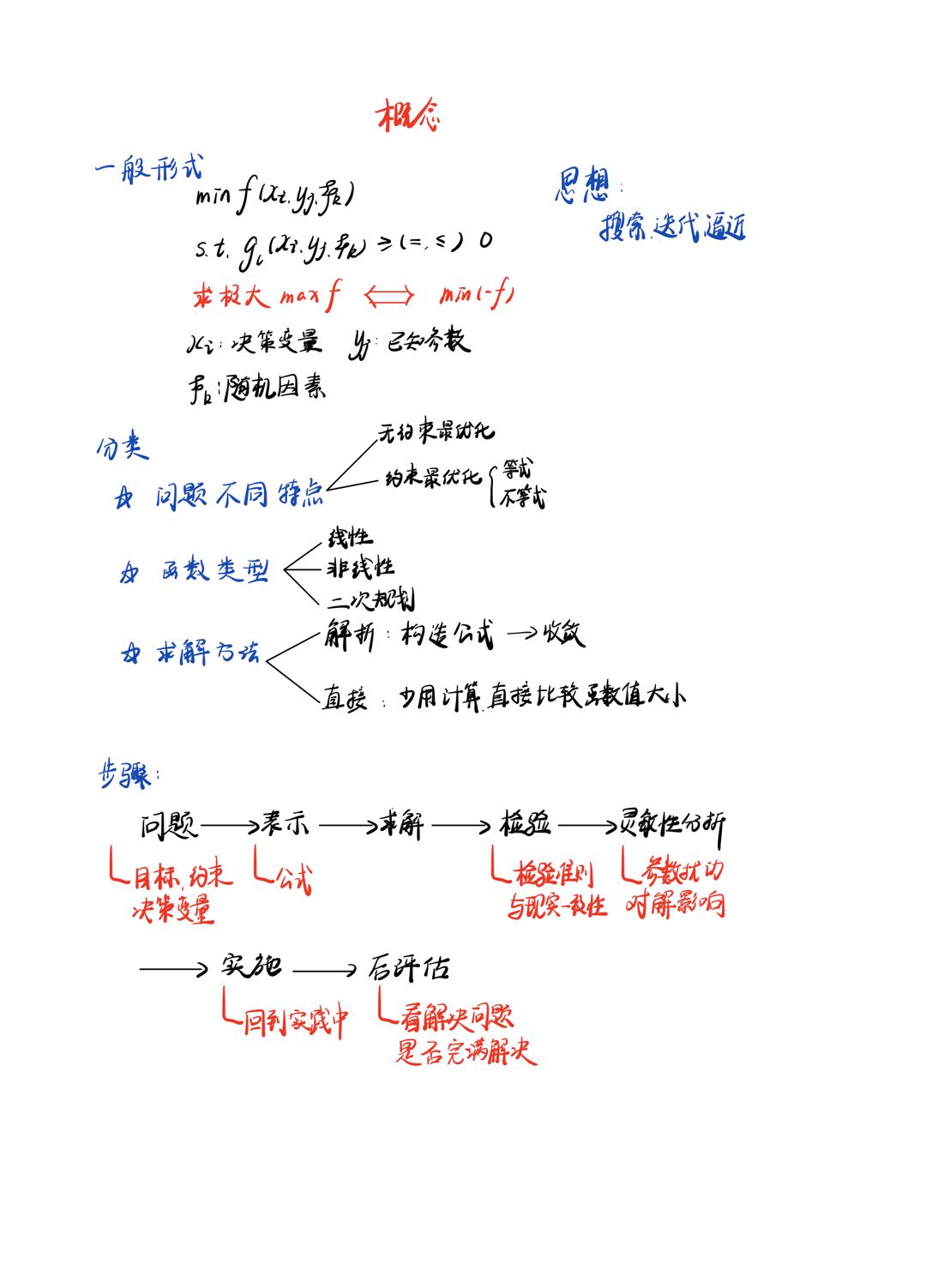
$一元优化问题$

$全局最优化$

$多元方程求根$

$最小二乘法$

$无约束、带约束的多元优化算法$

二分法

def asdf(x):
    res=8*x**3-2*x**2-7*x+3 #修改函数
    return res

i=2 #迭代次数，自己修改
left=0,right=1
while i>0 :
    i = i-1
    ans = 0.1
    mid1 = (left + right + ans) / 2
    mid2 = (left + right - ans) / 2
    a=asdf(mid1)
    c=asdf(mid2)
    if a > c :
        right = mid1
    else :
        left = mid2

b=(left+right) / 2
print("左极限=%s,右极限=%s,极小值x=%s"%(left,right,b))

规划类

线性规划

使用第三方库:PULP，通过LpProblem建立优化问题，其函数原型如下

1	pulp.LpProblem(name='NoName', sense=LpMinimize)

函数参数：

1 2	name:用户自定义的问题名(用于输出信息) sense:LpMinimize(最小)/LpMaximize(最大)

例题

$max \quad f(x) = 2*x_1+ 3*x_2 - 5*x_3 \\ s.t.\quad x_1+3*x_2+x_3 <= 12 \\ \quad 2*x1-5*x_2+x_3>=10\\ \quad x_1+x_2+x_3 = 7\\ \quad x_1,x_2,x_3 >= 0\\$

代码

import pulp
MyProbLP  = pulp.LpProblem("LPProblemDemo01",sense=pulp.LpMaximize)
#决策变量
x1 = pulp.LpVariable('x1', lowBound=0, upBound=7, cat='Continuous') 
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7, cat='Continuous')
x3 = pulp.LpVariable('x3', lowBound=0, upBound=7, cat='Continuous') 
#目标函数
MyProbLP += 2*x1 + 3*x2 - 5*x3
#约束条件
MyProbLP += (2*x1 - 5*x2 + x3 >= 10)
MyProbLP += (x1 + 3*x2 + x3 <= 12)
MyProbLP += (x1 + x2 + x3 == 7)
#求解
MyProbLP.solve()
print("Status:", pulp.LpStatus[MyProbLP.status]) # 输出求解状态
for v in MyProbLP.variables():
    print(v.name, "=", v.varValue)  # 输出每个变量的最优值
print("F(x) = ", pulp.value(MyProbLP.objective))  #输出最优解的目标函数值

定义一个规划问题

1	MyProbLP = pulp.LpProblem("LPProbDemo1", sense=pulp.LpMaximize)

定义决策变量

1	x1 = pulp.LpVariable('x1', lowBound=0, upBound=7, cat='Continuous')

x1是用户定义的变量名。

参数 lowBound、upBound 用来设定决策变量的下界、上界；可以不定义下界/上界，默认的下界/上界是负无穷/正无穷。

参数 cat 用来设定变量类型，可选参数值：Continuous表示连续变量（默认值）、Integer 表示离散变量（用于整数规划问题）、 Binary 表示0/1变量（用于0/1规划问题）。

添加目标函数

1	MyProbLP += f(x)

添加目标函数使用 “问题名 += 目标函数式” 格式。

添加约束条件

1	MyProLP += g(t)

添加约束条件使用 “问题名 += 约束条件表达式” 格式。

求解

#模板
MyProbLP.solve()
    print("Status:", pulp.LpStatus[MyProbLP.status]) # 输出求解状态
    for v in MyProbLP.variables():
        print(v.name, "=", v.varValue)  # 输出每个变量的最优值
    print("F(x) = ", pulp.value(MyProbLP.objective))  #输出最优解的目标函数值

线性规划实例推荐

非线性

非线性规划实例推荐

例程：等式约束下的拉格朗日乘子法

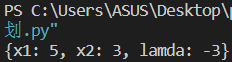
from sympy import *
#设置变量
x1 = symbols("x1")
x2 = symbols("x2")
lamda = symbols("lamda")
#构造拉格朗日等式
L = 60 - 10*x1 - 4*x2 + x1*x1 + x2*x2 - x1*x2 - lamda * (x1 + x2 - 8)
#求导，构造KKT条件
difyL_x1 = diff(L, x1) #x1偏导
difyL_x2 = diff(L, x2) #x2偏导
difyL_lamda = diff(L, lamda) #lamda偏导
#求解KKT等式
ans = solve([difyL_x1, difyL_x2, difyL_lamda], [x1, x2, lamda])
print(ans)

KKT条件讲解推荐

例程：模型构造

minimize() 函数中对约束条件的形式定义为 f(x)>=0，因此要将问题的数学模型转换为标准形式：

程序说明

参数a,b,c,d在子程序中直接赋值

定义边界约束

定义约束条件

$函数$ 对约束条件按照字典格式定义：

1
2
3

{‘type’: ‘ineq’, ‘fun’: functionname}
#‘type’ 的键值可选 ‘eq’ 和 ‘ineq’，分别表示的是约束和不等式约束
#functionname是定义约束条件的函数名

求解最小化问题 res

必需：目标函数、搜索初值点

可选：指定优化方法、边界条件、约束条件

通过调用最小化问题的返回值可以得到优化是否成功的说明（res.message）、自变量的优化值（res.x）和目标函数的优化值（res.fun）

函数：定义一个匿名函数，举个例子：我想定义一个实现加法的匿名函数并得到具体值，我就可以这样写：

1	add = lambda x,y : x+y

例程代码：

from scipy.optimize import brent, fmin, minimize
import numpy as np

# 5. Demo5：约束非线性规划问题(Scipy.optimize.minimize)
def objF5(args):  # 定义目标函数
    a,b,c,d = args
    fx = lambda x: a*x[0]**2 + b*x[1]**2 + c*x[2]**2 + d
    return fx

def constraint1():  # 定义约束条件函数
    cons = ({'type': 'ineq', 'fun': lambda x: (x[0]**2 - x[1] + x[2]**2)},  # 不等式约束 f(x)>=0
            {'type': 'ineq', 'fun': lambda x: -(x[0] + x[1]**2 + x[2]**3 - 20)},  # 不等式约束 转换为标准形式
            {'type': 'eq', 'fun': lambda x: (-x[0] - x[1]**2 + 2)},  # 等式约束
            {'type': 'eq', 'fun': lambda x: (x[1] + 2*x[2]**2 - 3)})  # 等式约束
    return cons

# 定义边界约束
b = (0.0, None)
bnds = (b, b, b)
# 定义约束条件
cons = constraint1()
args1 = (1,2,3,8)  # 定义目标函数中的参数
# 求解优化问题
x0 = np.array([1., 2., 3.])  # 定义搜索的初值
res1 = minimize(objF5(args1), x0, method='SLSQP', bounds=bnds, constraints=cons)

print("Optimization problem (res1):\t{}".format(res1.message))  # 优化是否成功
print("xOpt = {}".format(res1.x))  # 自变量的优化值
print("min f(x) = {:.4f}".format(res1.fun))  # 目标函数的优化值

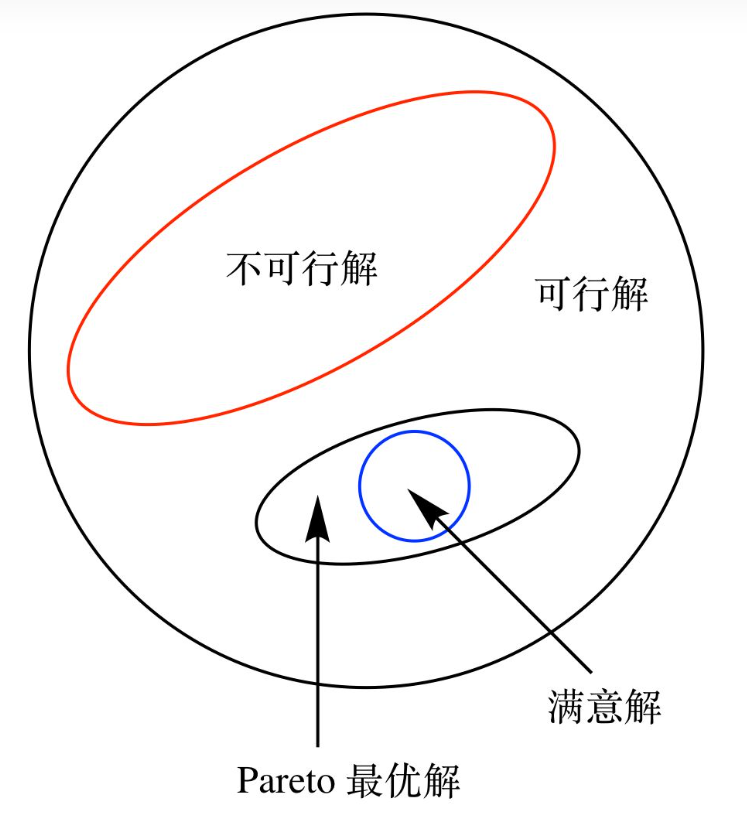
多目标优化

在生活中的优化问题，往往不只有一个优化目标，并且往往无法同时满足所有的目标都最优，我们一般采用“帕累托最优”来衡量解是否优秀。

帕累托最优：指资源分配的一种理想状态。假定固有的一群人和可分配的资源，从一种分配状态到另一种状态的变化中，在没有使任何人境况变坏的前提下，使得至少一个人变得更好。帕累托最优状态就是不可能再有更多的帕累托改进的余地

多目标进化优化算法即利用进化算法结合多目标优化策略来求解多目标优化问题。经典而久经不衰的多目标优化算法有：NSGA2、NSGA3、MOEA/D等。其中NSGA2和NSGA3是基于支配的MOEA(Multi-objective evolutionary algorithm)，而MOEA/D是基于分解的MOEA。

常用模型：

$线性加权$

对于第个目标函数，对应的权重为，最后相加即可。线性加权法严格意义上和“加权求和”一致，是把多目标优化转换成单目标问题解决，而由于无法精准确定权重，以及线性相加缺乏理论基础，主要适用于多个评价指标相互独立的情况，但是由于过程简单便捷，目前被广泛应用。

$基于相互关系$

上面是计算机网络中延迟和吞吐量综合优化过程中常用的Power公式，可以用来评价网络中资源分配策略的有效性，用以确定最优负载；亦可用来评价Web服务的效率。

$帕累托最优$

[1]唐云岚,赵青松,高妍方,陈英武.Pareto最优概念的多目标进化算法综述[J].计算机科学,2008(10):25-27+57.

不需要对目标进行缩放和归一化，也不需要设定或者引入新的参数、变量(如权重、界限值)，直接基于原始目标函数和值进行操作，可以适用于任何目标、任何函数．它不会丢失目标函数和解的信息，解的优劣可以较好保证。但帕累托模型的最优解是一个集合，其中包含不止一个最优解，因此要穷尽并求出所有的帕累托最优解有一定的难度。

常用解法与推荐论文：

$进化算法$

[1]公茂果,焦李成,杨咚咚,马文萍.进化多目标优化算法研究[J].软件学报,2009,20(02):271-289.

$神经网络$

[1]马永杰,云文霞.遗传算法研究进展[J].计算机应用研究,2012,29(04):1201-1206+1210.

$粒子群算法$

[1]张利彪,周春光,马铭,刘小华.基于粒子群算法求解多目标优化问题[J].计算机研究与发展,2004(07):1286-1291.

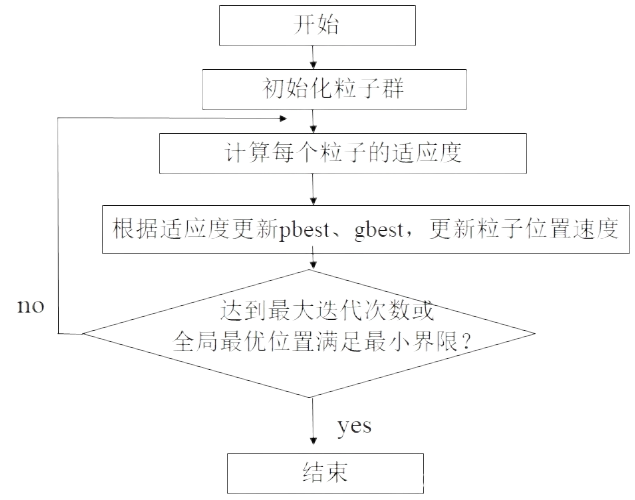
粒子群算法的思想源于对鸟类捕食行为的研究，模拟鸟集群飞行觅食的行为，鸟之间通过集体的协作使群体达到最优目的。 设想这样的一个场景，一群鸟在随机的搜索食物，在某块区域里有一块食物，所有的鸟都不知道食物在哪里，但是他们可以感受到当前的位置离食物还有多远，此时找到食物的最优策略是什么？

答案是：搜寻目前离食物最近的鸟的周围区域，根据自己的飞行经验判断食物的所在。