Meta Field
0%

微分方程

发表于 更新于 分类于 Valine：
本文字数： 6.9k 阅读时长 ≈ 6 分钟

微分方程建模

模型找教材，建模找例题，求解有例程，讨论有套路，论文够档次。

微分方程数值解法

思想：把时间和空间离散化，然后将微分化为差分，建立递推关系，然后反复进行迭代计算，得到任意时间和空间的值。

工具选择

是语言的，包括最优化、线性代数、积分、插值、特殊函数、傅里叶变换、信号和图像处理、常微分方程求解等模块。

专攻高维数组实现与计算，如线性代数运算、傅里叶变换及随机数生成模块。

可视化工具包，可以方便地绘制各种数据可视化图表，如折线图、散点图、直方图、条形图、箱形图、饼图、三维图，等等。

给出的结果是微分方程的解析解表达式，但是很少用。

常微分方程编程步骤

导包

定义导数函数

定义初值的定义区间

调用 odeint()求数值解

一阶常微分方程（组）

img

式中的 y 在常微分方程中是标量，在常微分方程组中是数组向量。

例程一阶常微分方程数值解

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 1. 求解微分方程初值问题(scipy.integrate.odeint)
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt

def dy_dt(y, t):  # 定义函数 f(y,t)
    return np.sin(t**2)

y0 = [1]  # y0 = 1 也可以
t = np.arange(-10,10,0.01)  # (start,stop,step)
y = odeint(dy_dt, y0, t)  # 求解微分方程初值问题

# 绘图
plt.plot(t, y)
plt.title("scipy.integrate.odeint")
plt.show()

img

例程一阶常微分方程组数值解

方程

img

导包

定义导数函数

1
2
3
4
5
6
7
#定义导数函数，求W=[x,y,z]点的导数
def lorenz(W,t,p,r,b):
    x, y, z = W  # W=[x,y,z]
    dx_dt = p*(y-x)  # dx/dt = p*(y-x), p: sigma
    dy_dt = x*(r-z) - y  # dy/dt = x*(r-z)-y, r:rho
    dz_dt = x*y - b*z  # dz/dt = x*y - b*z, b;beta
    return np.array([dx_dt,dy_dt,dz_dt])

定义初值和的区间

调用 odeint()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 2. 求解微分方程组初值问题(scipy.integrate.odeint)
from scipy.integrate import odeint    # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 导数函数, 求 W=[x,y,z] 点的导数 dW/dt
def lorenz(W,t,p,r,b):  # by youcans
    x, y, z = W  # W=[x,y,z]
    dx_dt = p*(y-x)  # dx/dt = p*(y-x), p: sigma
    dy_dt = x*(r-z) - y  # dy/dt = x*(r-z)-y, r:rho
    dz_dt = x*y - b*z  # dz/dt = x*y - b*z, b;beta
    return np.array([dx_dt,dy_dt,dz_dt])

t = np.arange(0, 30, 0.01)  # 创建时间点 (start,stop,step)
paras = (10.0, 28.0, 3.0)  # 设置 Lorenz 方程中的参数 (p,r,b)

# 调用ode对lorenz进行求解, 用两个不同的初始值 W1、W2 分别求解
W1 = (0.0, 1.00, 0.0)  # 定义初值为 W1
track1 = odeint(lorenz, W1, t, args=(10.0, 28.0, 3.0))  # args 设置导数函数的参数
W2 = (0.0, 1.01, 0.0)  # 定义初值为 W2
track2 = odeint(lorenz, W2, t, args=paras)  # 通过 paras 传递导数函数的参数

# 绘图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2], color='magenta') # 绘制轨迹 1
ax.plot(track2[:,0], track2[:,1], track2[:,2], color='deepskyblue') # 绘制轨迹 2
ax.set_title("Lorenz attractor by scipy.integrate.odeint")
plt.show()

img

例程二阶电路数值解

img

令：

，对于零输入响应可以将上述式子改写为：

img

引入变量，替换变量得：

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# 3. 求解二阶微分方程初值问题(scipy.integrate.odeint)
# Second ODE by scipy.integrate.odeint
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt

# 导数函数，求 Y=[u,v] 点的导数 dY/dt
def deriv(Y, t, a, w):
    u, v = Y  # Y=[u,v]
    dY_dt = [v, -2*a*v-w*w*u]
    return dY_dt

t = np.arange(0, 20, 0.01)  # 创建时间点 (start,stop,step)
# 设置导数函数中的参数 (a, w)
paras1 = (1, 0.6)  # 过阻尼：a^2 - w^2 > 0
paras2 = (1, 1)  # 临界阻尼：a^2 - w^2 = 0
paras3 = (0.3, 1)  # 欠阻尼：a^2 - w^2 < 0

# 调用ode对进行求解, 用两个不同的初始值 W1、W2 分别求解
Y0 = (1.0, 0.0)  # 定义初值为 Y0=[u0,v0]
Y1 = odeint(deriv, Y0, t, args=paras1)  # args 设置导数函数的参数
Y2 = odeint(deriv, Y0, t, args=paras2)  # args 设置导数函数的参数
Y3 = odeint(deriv, Y0, t, args=paras3)  # args 设置导数函数的参数
# W2 = (0.0, 1.01, 0.0)  # 定义初值为 W2
# track2 = odeint(lorenz, W2, t, args=paras)  # 通过 paras 传递导数函数的参数

# 绘图
plt.plot(t, Y1[:, 0], 'r-', label='u1(t)')
plt.plot(t, Y2[:, 0], 'b-', label='u2(t)')
plt.plot(t, Y3[:, 0], 'g-', label='u3(t)')
plt.plot(t, Y1[:, 1], 'r:', label='v1(t)')
plt.plot(t, Y2[:, 1], 'b:', label='v2(t)')
plt.plot(t, Y3[:, 1], 'g:', label='v3(t)')
plt.axis([0, 20, -0.8, 1.2])
plt.legend(loc='best')
plt.title("Second ODE by scipy.integrate.odeint")
plt.show()

img

基本模型

Malthus模型

S型曲线，与现实不符，基本用不上（x

Logistic模型

就是高中那个S型曲线，由Malthus模型修改而来，在模型中增加一个竞争项

从统计学来看，选取竞争项为，于是修改为：

img

代码实现

1
2
3
4
def logistic_Increase_Model(t,K,P0,r):
    # t:time   t0:initial_time    P0:initial_value    K:capacity  r:increasing_rate
    exp_value=np.exp(r*(t-t0))
    return (K*exp_value*P0)/(K+(exp_value-1)*P0)

例程代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#到时候更改数据即可
import math
import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

def logistic_increase_function(t,K,P0,r):
    # t:time   t0:initial time    P0:initial_value    K:capacity  r:increase_rate
    t0=11  
    r=0.6
    exp_value=np.exp(r*(t-t0))
    return (K*exp_value*P0)/(K+(exp_value-1)*P0)

#  日期及感染人数
t=[11,18,19,20,21,22,23,24,25,26,27]
t=np.array(t)
P=[41,45,62,291,440,571,830,1287,1975,2744,4515]
P=np.array(P)

# 用最小二乘法估计拟合
popt, pcov = curve_fit(logistic_increase_function, t, P)
# popt - K,P0,r
# 最终K=4.01665705e+10人会被感染
# array([7.86278276e+03, 2.96673434e-01, 1.00000000e+00])

#获取popt里面是拟合系数
print("K:capacity  P0:initial_value   r:increase_rate   t:time")
print(popt)

#拟合后预测的P值
P_predict = logistic_increase_function(t,popt[0],popt[1],popt[2])

#未来预测
future=[11,18,19,20 ,21, 22, 23, 24,  25,  26,  27,28,29,30,31,41,51,61,71,81,91,101]
future=np.array(future)
future_predict=logistic_increase_function(future,popt[0],popt[1],popt[2])

#近期情况预测
tomorrow=[28,29,30,32,33,35,37,40]
tomorrow=np.array(tomorrow)
tomorrow_predict=logistic_increase_function(tomorrow,popt[0],popt[1],popt[2])

#绘图
plot1 = plt.plot(t, P, 's',label="confimed infected people number")
plot2 = plt.plot(t, P_predict, 'r',label='predict infected people number')
plot3 = plt.plot(tomorrow, tomorrow_predict, 's',label='predict infected people number')
plt.xlabel('time')
plt.ylabel('number')
plt.legend(loc=0) #指定legend的位置右下角

#print(logistic_increase_function(np.array(28),popt[0],popt[1],popt[2]))
#print(logistic_increase_function(np.array(29),popt[0],popt[1],popt[2]))

#未来预测绘图
#plot2 = plt.plot(t, P_predict, 'r',label='polyfit values')
#plot3 = plt.plot(future, future_predict, 'r',label='polyfit values')

plt.show()
print("Program done!")

img

高斯拟合例程代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import math


#自定义高斯函数
def func(x, a,u, sig):
    return  a*(np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig))


#定义x、y散点坐标
x = [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]
x=np.array(x)
print('x is :\n',x)
num = [365,398,480,619,705,761,752,668,722,888,730,707,696,544,505,442,370,377,311,267,221,165,115,81,56]
y = np.array(num)
print('y is :\n',y)

popt, pcov = curve_fit(func, x, y,p0=[0,1,2])
#获取popt拟合系数
a = popt[0]
u = popt[1]
sig = popt[2]

yvals = func(x,a,u,sig) #拟合y值
print('系数a:', a)
print('系数u:', u)
print('系数sig:', sig)
#绘图
plt.rcParams['font.sans-serif']=['SimHei']
plt.xlabel('统计天数')
plt.ylabel('人数')
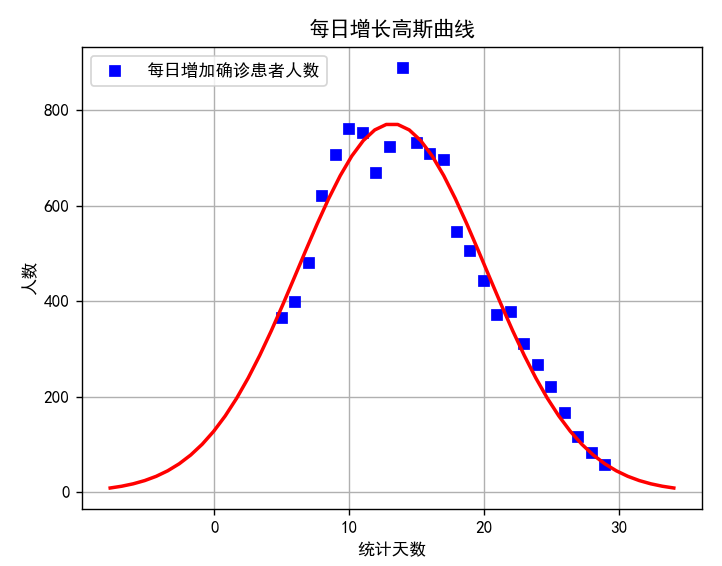
plot1 = plt.plot(x, y, 's',label='每日增加确诊患者人数',color='blue')
x = np.linspace(u - 3*sig, u + 3*sig, 50)
x_01 = np.linspace(u - 6 * sig, u + 6 * sig, 50)
y_sig = a* ( np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig) )
plt.plot(x, y_sig, "r-", linewidth=2)
# plt.plot(x, y, 'r-', x, y, 'go', linewidth=2,markersize=8)
plt.grid(True)
plt.legend(loc=2)
plt.title('每日增长高斯曲线')
plt.show()

img

SIS与SIR模型

SIS

SIR

-------------本文结束感谢您的阅读-------------
请作者喝一杯蜜雪冰城吧！