Genetic Algorithm Introduction Genetic Algorithms are categorized as global search heuristics. A genetic algorithm is a search technique used in computing to find true or approximate solutions to optimization and search problems. It uses techniques inspired by biological evolution such as inheritance, mutation, selection, and crossover.
①群智能:由简单个体组成的群落与环境以及个体之间的互动行为
②遗传算法本质上是一种群智能算法,强调以种群的达尔文主义进化模型为基础
③遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法
Explanations of Terms
xxxxxxxxxx4 1SELECT columns FROM table2ORDER BY column; #升序3SELECT columns FROM table4ORDER BY column DESC; #降序sql
Principles of the Algorithm 遗传算法五个基本要素🖐 1.参数编码
2.初始群体设定
3.适应度函数的设计
4.遗传操作设计
5.控制参数设计
1.参数编码(难点)
通过编码将要求解的问题表示成 遗传空间的染色体或者个体,编码方式有很多种,对特定问题采用特殊方法。
编码原则 1.完备性completeness:问题空间(表现型)的所有解都能表示为所设计的基因型
2.健全性soundness:任何一个基因型都对应于一个可能解
3.非冗余性non-redundancy:问题空间(表现型)和表达空间(基因型)一一对应
主流编码方法 ①二进制编码 类似于生物染色体组成,将若干二进制数表示成一个个体,原问题的解空间映射到位串空间B={0,1}上,然后在位串空间上进行遗传操作。
👍优点:编解码简单;算法易于用生物遗传理论来解释和操作。
👎缺点:对于一些连续函数的优化问题,由于其随机性使其局部搜索能力差,当接近最优解时,由于变异后表现型变化很大,不连续,所以会远离最优解;求解高维问题时搜索效率低。
举例:
染色体0010101111就可以表示表现型为x=175的个体。
拓展1.python 2进制<===>10进制✍
先转换为字符串,又因为是2进制为基础,所以第二个参数是2
拓展2.编解码映射公式✍
encoding_num:解码数 decoding_num:编码数
num:需要编码的数
var_num:当前范围下限 var_len:当前变量取值范围长度
DNA_SIZE:DNA长度,即碱基对个数
②实数编码 若干实数表示一个个体,在实数空间进行遗传操作。
近年来,遗传算法在求解高维问题或复杂优化问题时一般用实数编码。
2.初始群体设定 随机产生,规模一般在20-100个个体左右
·数量过少->局部最优解
·数量过多->计算复杂
3.适应度函数设计 适应度:度量某个物种对于生存环境的适应程度。
适应度函数表明:个体或解的优劣性 。
一般而言,适应度函数是由目标函数变换得到的。
(1)直接将目标函数作为适应度函数 (2)倒数法 🔨c是目标函数界限的保守估计值
👉它是依据一定理由 估算的一个大概数,严格地说它并不等于最少或最低 。
4.遗传操作设计(遗传算子) ① Φ:选择算子
选择操作从旧群体中以一定概率选择优良个体组成新的种群,以繁殖得到下一代个体。个体被选中的概率跟适应度值有关,个体适应度值越高,被选中的概率越大。
最常用:轮盘赌选择(roulette wheel selections,RWS)
若个体的选择概率大,则有机会被多次选中,那么它的遗传基因就会在种群中扩大;若个体的选择概率小,则被淘汰的可能性会大。
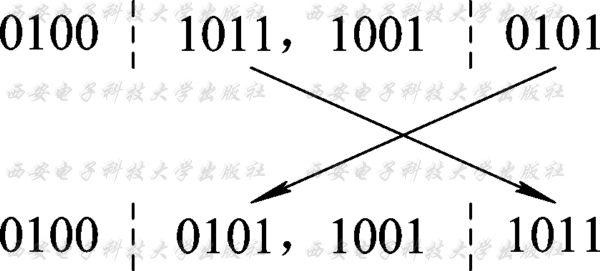
② Γ:交叉算子
交叉操作是指从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体。
③ ψ:变异算子
在实际应用中,主要采用单点变异,也叫位变异,即只需要对基因序列中某一个位进行变异,以二进制编码为例,即0变为1,而1变为0 。
5.控制参数设计 遗传算法有4个运行参数需要预先设定
Code Implementation Examples Eg1: Crack a Password Using a Genetic Algorithm(Base Level) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 import random import datetime def generate_parent (length ): genes = [] while len (genes) < length: sampleSize = min (length-len (genes),len (geneSet)) genes.extend(random.sample(geneSet,sampleSize)) return '' .join(genes) def get_fitness (guess ): return sum (1 for excepted , actual in zip (target,guess) if excepted == actual) def mutate (parent ): index = random.randrange(0 ,len (parent)) childGenes = list (parent) newGene , alternate = random.sample(geneSet,2 ) childGenes[index] = alternate if newGene == childGenes[index] else newGene return '' .join(childGenes) def display (guess ): timeDiff = datetime.datetime.now() - startTime fitness = get_fitness(guess) print ("{0}\t{1}\t{2}" .format (guess, fitness, str (timeDiff))) random.seed() geneSet = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ" target = "Anh" startTime = datetime.datetime.now() bestParent = generate_parent(len (target)) bestFitness = get_fitness(bestParent) display(bestParent) while True : child = mutate(bestParent) childFitness = get_fitness(child) if bestFitness >= childFitness: continue display(child) if childFitness >= len (bestParent): break bestFitness = childFitness bestParent = child
代码解释👇
1.datetime🕐
⚙Basic date and time types
datetime模块重新封装了time模块,提供更多的接口
官方文档
详解+示例
2.join()🛶
⚙语法
参数
sequence—要连接的元素序列
返回值
返回通过指定字符连接序列中元素后生成的新字符串。
3.format()格式化函数🎫
⚙语法
1 2 3 4 str .format () print ("{0}\t{1}\t{2}" .format (guess, fitness, str (timeDiff)))
📋b,d,o,x 分别是二进制、十进制、八进制、十六进制。
4.list()函数
✍它可以将任何可迭代数据转换为列表类型,并返回转换后的列表。当参数为空时,list函数可以创建一个空列表。
实例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 >>> test = list () >>> test [] >>> test = list ('cat' ) >>> test ['c' , 'a' , 't' ] >>> a_tuple = ('I love Python.' , 'I also love HTML.' ) >>> test = list (a_tuple) >>> test ['I love Python.' , 'I also love HTML.' ] >>> a_dict = {'China' :'Beijing' , 'Russia' :'Moscow' } >>> test = list (a_dict) >>> test ['China' , 'Russia' ] >>> a_set = {1 , 4 , 'sdf' } >>> test = list (a_set) >>> test [1 , 'sdf' , 4 ] >>> test1 = list (range (10 )) >>> test2 = list (map (int , [23.2 , 33.1 ])) >>> test1 [0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ] >>> test2 [23 , 33 ]
5.正斜杠/与反斜杠\
👋除号是正斜杠
👋对于目录分隔符,Unix和Web用/,Windows用\。
6.extend()函数
📋用于在列表末尾一次性追加另一个序列中的多个值(用新列表扩展原来的列表)。
⚙语法
👋该方法没有返回值,但会在已存在的列表中添加新的列表内容。
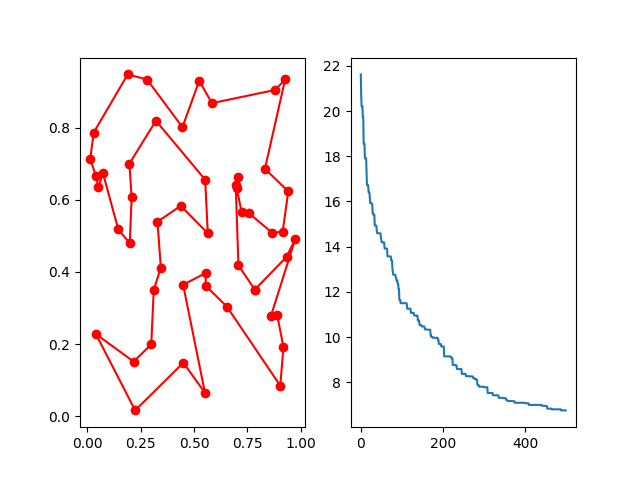
Eg2:Application of GA - Traveling Salesman Problem(TSP) 这是一个经典的组合优化问题。
可描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短。
这里使用scikit-opt库 实现,后续会更新这道题目的详解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 import numpy as np from scipy import spatial import matplotlib.pyplot as plt num_points = 50 points_coordinate = np.random.rand(num_points, 2 ) distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean' ) def cal_total_distance (routine ): '''The objective function. input routine, return total distance. cal_total_distance(np.arange(num_points)) ''' num_points, = routine.shape return sum ([distance_matrix[routine[i % num_points], routine[(i + 1 ) % num_points]] for i in range (num_points)]) from sko.GA import GA_TSP ga_tsp = GA_TSP(func=cal_total_distance, n_dim=num_points, size_pop=50 , max_iter=500 , prob_mut=1 ) best_points, best_distance = ga_tsp.run() fig, ax = plt.subplots(1 , 2 ) best_points_ = np.concatenate([best_points, [best_points[0 ]]]) best_points_coordinate = points_coordinate[best_points_, :] ax[0 ].plot(best_points_coordinate[:, 0 ], best_points_coordinate[:, 1 ], 'o-r' ) ax[1 ].plot(ga_tsp.generation_best_Y) plt.show()