SVM

SVM需要大量的数学理论基础，推导和原理很麻烦但是有趣，为了让大家看的更舒服一些，笔者干脆整了个活；理解SVM总共有三层境界，受笔者数学水平所限，只能理解两层，第三层境界是证明SVM，欢迎大佬们来🔨

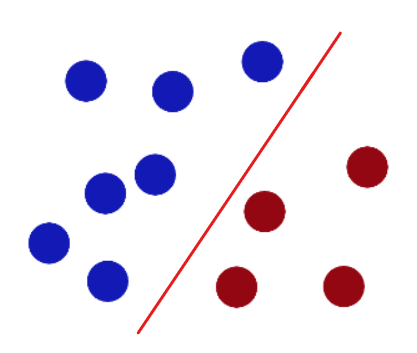
基础

先问是什么

蔡徐坤送给你很多🏀和🐔，现在你在操场上要进行分类，是这样分布的：

KUN说：聪明的你，一定知道怎样把它们分类对吧？我希望，你把🏀和🐔联系起来想一想，嗯？🤾‍♂️

哦！你画一条线就可以了！

不过KUN哥故意多放一只🐔，这只🐔开始打篮球了，这该怎么办腻？

于是你的CPU借助了图灵之力，又重新画了一条线，这样问题就解决了。不过KUN哥并不打算放过这个小黑子：“这样你会么？”

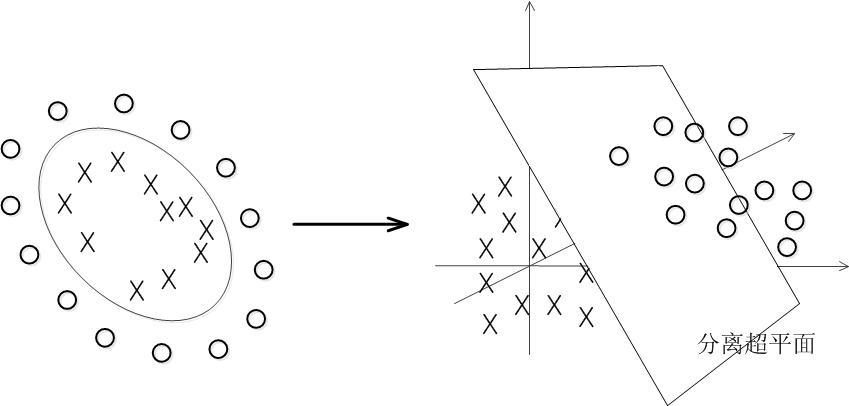
画直线不好使，那画一条曲线总可以吧，但是直接画不太妥，所以你直接一个铁山靠，将🏀和🐔从操场上靠飞了，然后你就像水果忍者一样，在空间中切出一个平面：

后来，这个故事在IKUN圈广泛流传，小黑子们把🏀和🐔统称为数据data，线称classifier，最大间隙叫optimization，操场叫做hyperplane，切法叫做Dimensionality reduction。

好，你明白这是个啥了，那么具体理论要开始给你洗脑了。

梦开始的地方

👉《🍉📒》

给定训练样本集,{} 。

样本空间中，划分超平面按照如下线性方程来描述：

$$\pmb {w^T} \pmb x + b \, = \, 0$$

这个式子怎么理解呢？

ML中，向量默认为列向量，我们可以假设都是二维向量,,然后把代进去展开

$$w_1x_1+w_2x_2+b = 0$$

🧐这不是初中数学嘛？

样本中任意点到超平面距离可以写为

$$r = \frac{\pmb {w^Tx}+b}{||\pmb{w}||}$$

这个展开就类似二维空间中的距离公式

$$d = \frac{Ax_1+By_1+C}{\sqrt{A^2+B^2}}$$

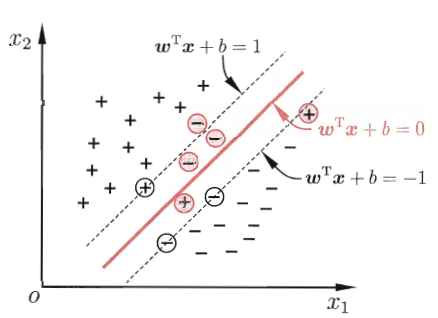
假设超平面能将训练样本正确分类，即

$$\begin{cases} \pmb {w^Tx_i}+b \ge +1,y_i = +1 \\ \pmb {w^Tx_i}+b \le -1,y_i = -1 \end{cases}$$

距离超平面最近的这几个训练点使得最短距离就是分子取最小值为1，这样的点被称为“支持向量”(support vector)，两个异类支持向量到超平面距离之和为

$$\gamma = \frac{2}{||\pmb w||}$$

也被称为“间隔”(margin)

我们想做的是找到具有最大间隔的划分超平面，也就是取最大值，有如下式子

$$max_{\pmb w,b}\quad \frac{2}{||\pmb w||} \\ s.t. y_i(\pmb{w^Tx_i}+b) \ge 1 , i=1,2,\dots,m$$

当然可以重写为

$$min_{\pmb w,b}\quad \frac{1}{2}||\pmb w||^2 \\ s.t. y_i(\pmb{w^Tx_i}+b) \ge 1 , i=1,2,\dots,m$$

👋平方是去掉根号，为了方便计算

👆就是SVM基本型

继续深入

凸二次规划

看到这个概念可能很陌生，不过你已经学过高数了，你一定还记得凸函数是什么

$$f(\frac{x_1+x_2}{2}) \le \frac{[f(x_1)+f(x_2)]}{2}$$

严格凸函数没有等号，典型例子是

还有一个仿射函数：最高次数为1的多项式函数，形如。仿射函数也是凸函数，但不是严格凸函数。常数项为零的仿射函数称为线性函数，线性函数是过原点的仿射函数。

凸函数和仿射函数在一起就有了凸优化问题，如下定义：

是目标函数且为凸函数，是不等式约束且为凸函数，是等式约束且为仿射函数，三者定义域内连续可微。

凸二次规划是凸优化的一个特殊形式，当目标函数是二次型函数且不等式约束函数是仿射函数时，就变成一个凸二次规划问题。

核心思想：在一定的约束条件下，目标最优，损失最小。

SVM就是典型的凸二次规划。

拉格朗日乘数法

大一学的针对等式优化，这里只针对不等式优化进行分析。

主要思想是将不等式约束条件转变为等式约束条件，引入松弛变量，将松弛变量也看作优化变量。

$$min\quad f(w) = min \quad \frac{1}{2}||w||^2$$ $$s.t.\quad g_i(w) = 1-y_i(w^Tx_i+b) \leq 0$$

引入松弛变量得到。

✍这里加平方主要为了不再引入新的约束条件，如果单单引入,那么我们必须保证才能保证,不符合我们的意愿。

由此我们得到Lagrange 函数

$$L(w,\lambda,a)=f(w)+\sum_{i=1}^{n}\lambda_i[g_i(w)+a_i^2]\quad \lambda_i \ge 0$$

我们对分别求偏导，联立方程

$$\begin{cases} \frac{\partial L}{\partial w_i} = \frac{\partial f}{\partial w_i} + \sum_{i=1}^{n} \lambda_i \frac{\partial g_i}{\partial w_i} =0 , \\ \frac{\partial L}{\partial a_i} = 2\lambda_ia_i = 0 ,\\ \frac{\partial L}{\partial \lambda_i} = g_i(w)+a_i^2 = 0,\\ \lambda_i \ge 0 \end{cases}$$

针对有两种情况：

①

约束条件不起作用

②

约束条件起作用且

综上，,且在约束条件起作用时,;约束不起作用时。

所以方程组转化为

$$\begin{cases} \frac{\partial L}{\partial w_i} = \frac{\partial f}{\partial w_i} + \sum_{i=1}^{n} \lambda_i \frac{\partial g_i}{\partial w_i}=0 , \\ \lambda_ig_i(w) = 0 , \\ g_i(w) \le 0 \\ \lambda_i \ge 0 \end{cases}$$

这就是大名鼎鼎的KKT条件

从原问题到对偶问题

🔍对偶问题是什么？与原问题等价的问题。

📂转化后的优点？

①对偶问题往往更容易求解；

②可以自然的引入核函数，进而推广到非线性分类问题。

👆推导KKT就是典型的转化对偶问题。

KKT 条件是强对偶性的充要条件。

软间隔

在实际应用中，完全线性可分的样本是很少的，如果遇到了不能够完全线性可分的样本，我们应该怎么办？

所以我们提出一种解决方法：软间隔，允许个别🏀和🐔犯错误，也就是允许个别样本点出现在间隔带里面，为下一步核函数做铺垫。

核函数Kernel

省流版：对数据降维打击。

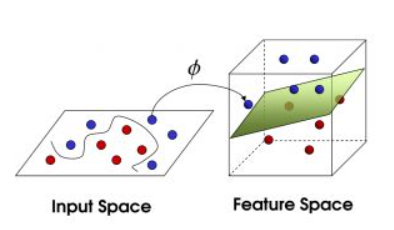
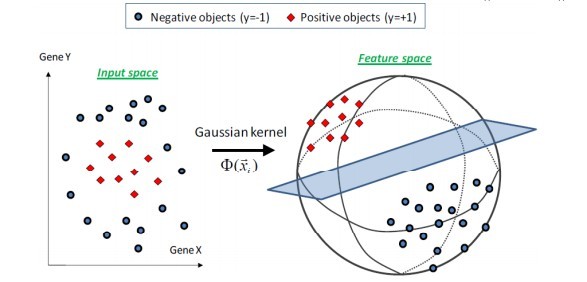
对于线性不可分的情况，SVM选择一个核函数，把数据扔到高维来解决原维度的线性不可分问题。

支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。

下面我们讲讲核函数具体怎么做了什么的。

比如我们在二维直角坐标系中取3个点，作为标记，对应的新特征命名为，我们要评价样本值与这些标记的相似度：

$$f_1 = similarity(x,l^{(1)})$$

计算相似度公式我们这样写

$$f_1 = exp(-\frac{||x-l^{(1)}||^2}{2\sigma^2})= exp(-\frac{\sum_{j=1}^{n}(x_j-l_j^{(1)})^2}{2\sigma^2})$$

if x near :

if x far from :

我在摸鱼的时候，你有在偷看概率论罢

对高斯分布一点也不陌生，我们把这种核函数叫高斯核，它的作用是升维计算。高斯核的使用关键在值的调整，过大会导致权重衰减非常快；反过来虽然可以将任意数据映射为线性可分，但是会导致严重的过拟合问题。高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。

下面是常用核函数

然后我们回到预测函数，假设我们知道的值并且有训练实例，判断是否0。对于大量的数据进行这样的处理，我们得到决策函数的判别边界，在红色圈里面预测值为1，外面为0。

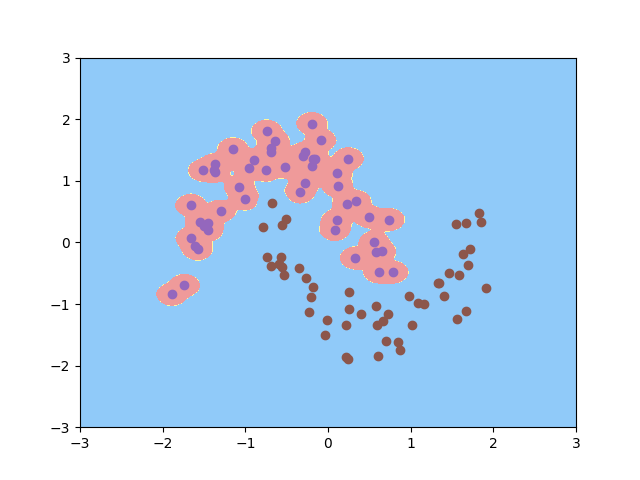
这样就得到了非线性的边界。

也就是说，SVM在处理非线性分类中具有非常强大的优势。

处理噪声outliers

引入松弛变量(slack variable)有,对应数据点允许偏离margin的量，所以我们在原来的目标函数后面加一项，叫做“正则项”使得总和最小。其中是一个参数，是事先确定好的常量，用于控制目标函数这两项之间的权重，相当于防止过拟合里的惩罚系数的作用，它越大，的值就得越小。

完整公式如下

$$min \quad\frac{1}{2}||w||^2+C\sum_{i=1}^{n}\varepsilon_i$$ $$s.t.\quad y_i(w^Tx_i+b) \ge 1 - \varepsilon_i , i=1,2,\dots,n$$ $$\varepsilon \ge 0 , i=1,2,\dots,n$$

同理，用上面的方法可以将限制或者约束条件加入到目标函数中，得到新的拉格朗日函数

$$L(w,b,\varepsilon,a,r)=\frac{1}{2}||w||^2+C\sum_{i=1}^{n}\varepsilon_i-\sum_{i=1}^{n}a_i(y_i(w^Tx_i+b)-1+\varepsilon_i)-\sum_{i=1}^{n}r_i\varepsilon_i$$

我们让针对最小化：

$$\begin{cases} \frac{\partial L}{\partial w} = 0 \Rightarrow \sum_{i=1}^{n}a_iy_ix_i = w \\ \frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{i=1}^{n}a_iy_i = 0 \\ \frac{\partial L}{\partial \varepsilon_i} = 0 \Rightarrow C-a_i-r^i =0 , i=1,\dots,n \end{cases}$$

将带回最后转化为

$$\begin{cases} max_a \sum_{i=1}^{n}a_i-\frac{1}{2}\sum_{i,j=1}^{n}a_ia_jy_iy_j <x_i,x_j>\\ s.t.\quad 0\le a_i \le C , i=1,\dots,n \\ \sum_{i=1}^{n}a_iy_i = 0 \end{cases}$$

Coding实现

分类模型举例

代码详解

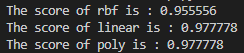
首先是3种SVM的准确性测试

from dataclasses import dataclass
from sklearn import svm
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split as ts

#load dataset
iris = load_iris()
x = iris.data
y = iris.target

#split dataset
x_train,x_test,y_train,y_test = ts(x,y,test_size=0.3)

#kernel = 'rbf'
clf_rbf = svm.SVC(kernel='rbf')
clf_rbf.fit(x_train,y_train)
score_rbf = clf_rbf.score(x_test,y_test)
print("The score of rbf is : %f"%score_rbf)

#kernel = 'linear'
clf_linear = svm.SVC(kernel='linear')
clf_linear.fit(x_train,y_train)
score_linear = clf_linear.score(x_test,y_test)
print("The score of linear is : %f"%score_linear)

#kernel = 'poly'
clf_poly = svm.SVC(kernel='poly')
clf_poly.fit(x_train,y_train)
score_poly = clf_poly.score(x_test,y_test)
print("The score of poly is : %f"%score_poly)

from sklearn import svm
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split as ts
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn import datasets
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt

moons = datasets.make_moons(noise=0.15)
X = moons[0]
y = moons[1]

plt.scatter(X[y==0,0], X[y==0, 1])
plt.scatter(X[y==1,0], X[y==1, 1])

def SVC_(kernel="rbf", gamma=1):
    return Pipeline([
        ("std_scaler", StandardScaler()),
        ("linearSVC", SVC(kernel="rbf", gamma=gamma))
    ])

svc = SVC_(kernel="rbf", gamma=0.7)
svc.fit(X, y)

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),# 600个，影响列数
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),# 600个，影响行数
    )
    # x0 和 x1 被拉成一列，然后拼接成360000行2列的矩阵，表示所有点
    X_new = np.c_[x0.ravel(), x1.ravel()]    # 变成 600 * 600行， 2列的矩阵

    y_predict = model.predict(X_new)   # 二维点集才可以用来预测
    zz = y_predict.reshape(x0.shape)   # (600, 600)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz,  cmap=custom_cmap)
#     print(X_new)


plot_decision_boundary(svc, [-3,3,-3,3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])

svc = SVC_(kernel="rbf", gamma=100)
svc.fit(X, y)

plot_decision_boundary(svc, [-3,3,-3,3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

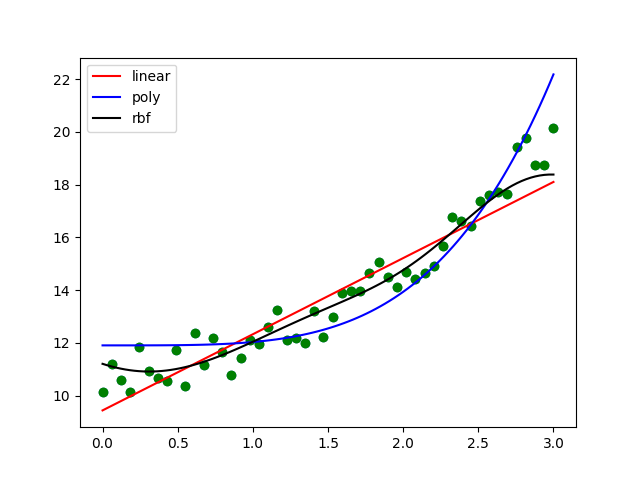
回归模型举例

SVM回归代码详解

import numpy as np
import matplotlib.pyplot as plt

from sklearn.svm import SVR
linear_svr = SVR(kernel="linear")
poly_svr = SVR(kernel="poly", degree=4)
rbf_svr = SVR(kernel="rbf")

x = np.linspace(0, 3, 50)
y = x * x + 10 + np.random.uniform(0,2,50)
x = x.reshape(-1,1)
plt.scatter(x,y)

linear_svr.fit(x,y)
poly_svr.fit(x,y)
rbf_svr.fit(x,y)

print(linear_svr.coef_, linear_svr.intercept_)    # [[2.62357607]] [10.14231851]

x_test = np.linspace(0,3,100).reshape(-1,1)
plt.scatter(x,y, color="green")
plt.plot(x_test, linear_svr.predict(x_test), color="red", label="linear")
plt.plot(x_test, poly_svr.predict(x_test), color="blue", label="poly")
plt.plot(x_test, rbf_svr.predict(x_test), color="black", label="rbf")
plt.legend()
plt.show()

评价

Advantages：

①有严格的数学理论支持，可解释性强，不依靠统计方法，从而简化了通常的分类和回归问题；

②采用核技巧之后，可以处理非线性分类/回归任务；

③能找出对任务至关重要的关键样本（即：支持向量）；

④最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了“维数灾难”。

Disadvantages：

①训练时间长。

②当采用核技巧时，如果需要存储核矩阵，则空间复杂度为 ；

③多分类存在困难，一般通过多个二类支持向量机组合来解决；

④模型预测时，预测时间与支持向量的个数成正比。当支持向量的数量较大时，预测计算复杂度较高。因此目前只适合小批量样本的任务，无法适应百万甚至上亿样本的任务。

后记

代码那里详解直接看链接网站