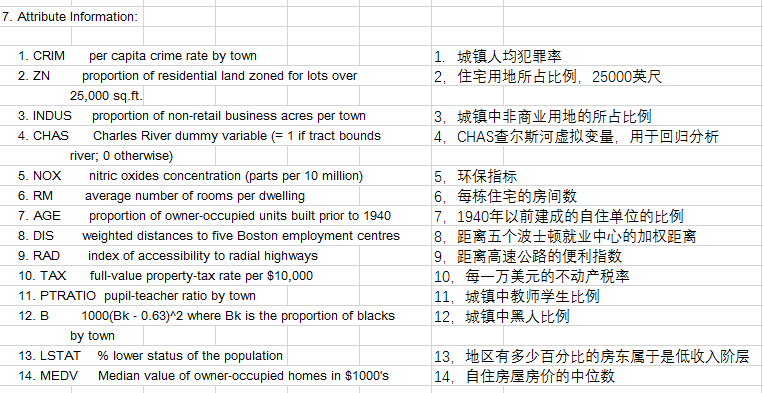
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
| import numpy as np
import seaborn as sns
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_boston
boston = load_boston()
X , y = boston.data,boston.target
feature_name = boston.feature_names
from sklearn.model_selection import train_test_split
X_train , X_test , y_train , y_test = train_test_split(X,y,test_size=0.2,random_state=0)
params = {'n_estimators': 500,
'max_depth': 3,
'min_samples_split': 5,
'learning_rate': 0.05,
'loss': 'ls'}
from sklearn.ensemble import GradientBoostingRegressor
GBDTreg = GradientBoostingRegressor(**params)
GBDTreg.fit(X_train,y_train)
y_predict = GBDTreg.predict(X_test)
mpl.rcParams['font.sans-serif'] = ['KaiTi', 'SimHei', 'FangSong']
mpl.rcParams['font.size'] = 12
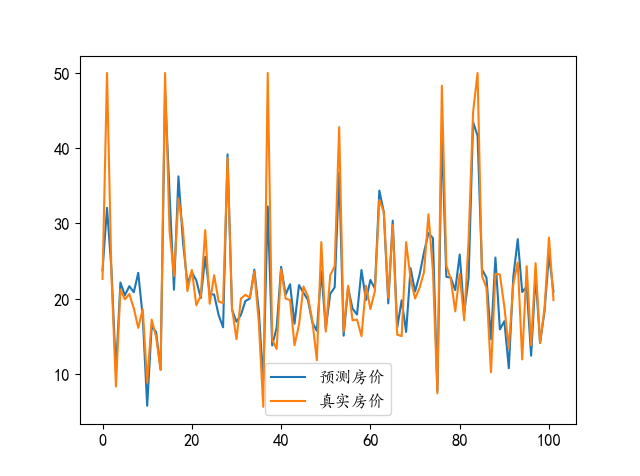
plt.plot(y_predict,label='预测房价')
plt.plot(y_test,label='真实房价')
plt.legend()
plt.show()
mse = mean_squared_error(y_test,y_predict)
print(mse)
test_score = np.zeros((params['n_estimators'],), dtype=np.float64)
for i, y_pred in enumerate(GBDTreg.staged_predict(X_test)):
test_score[i] = GBDTreg.loss_(y_test, y_predict)
fig = plt.figure(figsize=(6, 6))
plt.subplot(1, 1, 1)
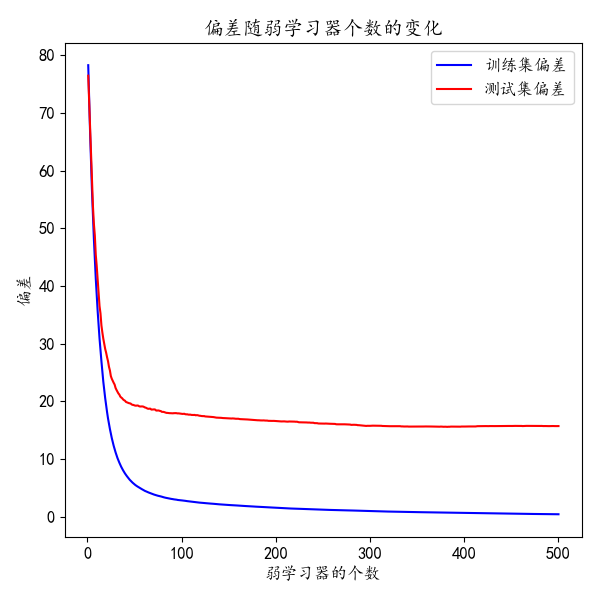
plt.title('偏差随弱学习器个数的变化')
plt.plot(np.arange(params['n_estimators']) + 1, GBDTreg.train_score_, 'b-',
label='训练集偏差')
plt.plot(np.arange(params['n_estimators']) + 1, test_score, 'r-',
label='测试集偏差')
plt.legend(loc='upper right')
plt.xlabel('弱学习器的个数')
plt.ylabel('偏差')
fig.tight_layout()
from sklearn.inspection import permutation_importance
feature_importance = GBDTreg.feature_importances_
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
fig = plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
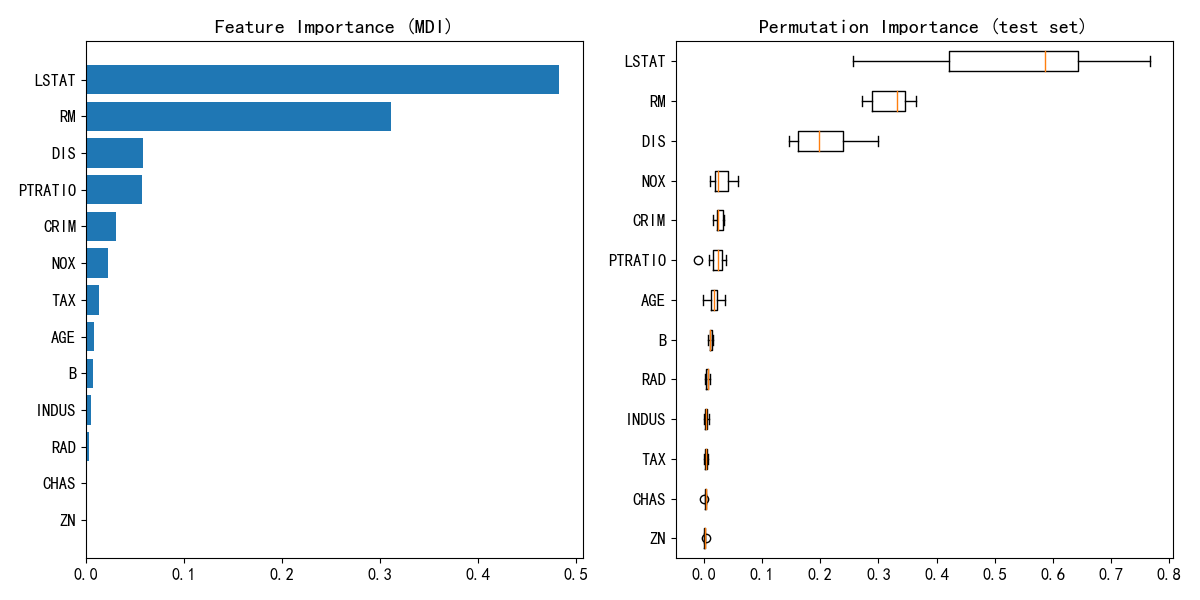
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, np.array(boston.feature_names)[sorted_idx])
plt.title('Feature Importance (MDI)')
result = permutation_importance(GBDTreg, X_test, y_test, n_repeats=10,
random_state=42, n_jobs=2)
sorted_idx = result.importances_mean.argsort()
plt.subplot(1, 2, 2)
plt.boxplot(result.importances[sorted_idx].T,
vert=False, labels=np.array(boston.feature_names)[sorted_idx])
plt.title("Permutation Importance (test set)")
fig.tight_layout()
plt.show()
|