组合数学

应该是第一篇专门总结数学的文章

参考教材

①《组合数学》西电出版社 姜建国

②《组合数学》机械工业出版社

③《组合数学》PekingU 冯荣权

组合数学基础

绪论

常用方法✍

①数学归纳法

②迭代法

③一一对应技术

④殊途同归方法

⑤数论方法

3，4是重点

排列与组合

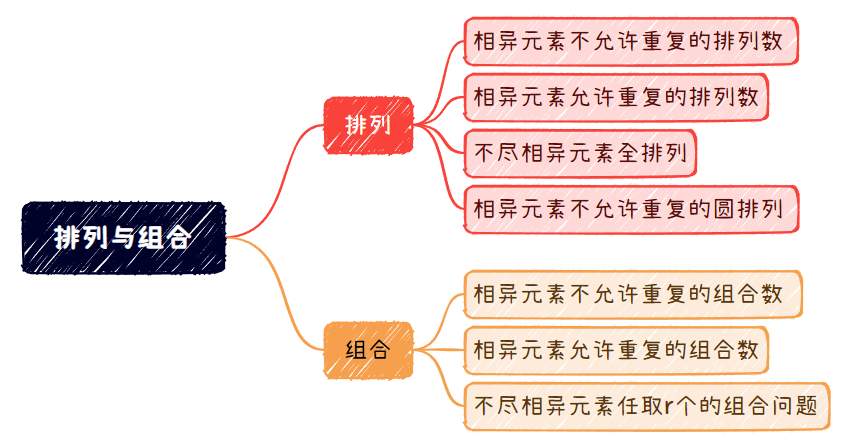
相异元素不允许重复的排列数(高中)

$$P_n^r = P(n,r)=n(n-1)(n-2) \dots (n-r+1)=\frac{n!}{(n-r)!}$$

相异元素允许重复的排列数

从集合角度好理解

设集合{}，即S中共含有n类元素，每类元素都有无穷多个，从S中取r个元素的排列数为。

不尽相异元素全排列

$$RP(n,n) = \frac{n!}{n_1!n_2!\dots n_t!}$$

直接上例子：

集合{}

1，2有2个；3有3个；5有1个

相异元素不允许重复的圆排列

🔨n个有标号的珠子排成一个圆圈，多少种不同排法

$$CP(n,n) = \frac{P(n,n)}{n}=(n-1)!$$

🔨n个相异元素不重复地取r个做圆排列，求不同排列总数

$$CP(n,r) = \frac{P(n,r)}{r}=\frac{n!}{r(n-r)!}$$

👆r个元素做圆排列，所以要除以r

🔨项链排列：从n个相异珠子取r个穿成一个项链，有👇多穿法

$$\frac{P(n,r)}{2r} = \frac{n!}{2r(n-r)!}$$

相异元素不允许重复的组合数(高中)

$$C_n^r = C(n,r) ={n\choose r} =\frac{P_n^r}{r!}=\frac{n!}{(n-r)!r!}$$

相异元素允许重复的组合问题

从集合角度好理解

设集合{}，从S中允许重复取r个元素构成组合，叫r可重组合，记作。

$$RC(\infty,r) = C(n+r-1,r) = \frac{(n+r-1)!}{r!(n-1)!}$$

将r个无区别的球放入n个不同的盒子，每个盒子球数不受限制。

不尽相异元素任取r个的组合问题

设集合{}，，从S中任取r个，求其组合数RC(n,r)

设多项式

$$\prod_{i=1}^{t} \sum_{j=0}^{n_i} x^j = \prod_{i=1}^{t}(1+x+x^2+\dots+x^{n_i}) = \sum_{r=0}^{n}a_rx^r$$

则RC(n,r)就是多项式中的系数，即。

正整数的约数个数为：

$$(\alpha_1+1)(\alpha_2+1)\dots(\alpha_k+1)$$

组合等式及其意义

乘法公式

$$C(n,k)C(k,r) = C(n,r)C(n-r,k-r)$$ $$C(n,n-k)C(k,k-r)C(r,r) = C(n,r)C(n-r,n-k)C(k-r.k-r)$$

等式4（书上就这样称呼）

$$C(n+r+1,r)=\sum_{i=0}^{r}C(n+i,i)$$

或

$$C(n+r+1,r) = \sum_{i=0}^{r}C(n+i,n)$$

从组合意义上来讲会更好理解，老师的讲解很重要：

这是一个递归的推导：

范德蒙等式

$$C(m+n,r) = \sum_{i=0}^{r}C(n,i)C(m,r-i)$$

组合意义：n个相异红球，m个相异篮球，从n+m个球中取r个的组合，其结果必是：i个红球，r-i个篮球。对固定的i，应有种选法，再来一个加法法则，得到上面的式子。

和式公式

$$\sum_{i=0}^{n}C(n,i) = 2^n$$

组合意义：对n个元素而言，每一个元素都有“取”和“不取”两种可能；等于：从n个元素中分别取0，1，，n个元素的总组合数。

等式7（我自己给他起名叫奇偶项公式）

$$\binom{n}{0}-\binom{n}{1}+\binom{n}{2}-\dots+(-1)^n\binom{n}{n}=0$$

组合意义：n个元素取r个组合，r为奇数的组合数目等于r为偶数的组合数目。(老师真的太厉害了！)

等式8

$$(C_{n}^{1})^2+2(C_{n}^{2})^2+\dots+n(C_{n}^{n})^2 = nC_{2n-1}^{n-1}$$

组合意义：从n名先生，n名女士选出n人，这n人里面1人担任主席，并且必须为女士，考虑有多少种选法。等式右面好理解，左面是重点。

对于,先从n名女士中选出k人，并从k人中选一个主席，是$kC{n}^{k}C{n}^{n-k}=C{n}^{k}\sum{k=1}^{n}k(C_{n}^{k})$种方法。

等式10

$$\sum_{k=0}^{n-m}C(n,m+k)C(m+k,m)=2^{n-m}C(n,m)$$

组合意义：从n个人中选m名正式代表以及若干名列席代表(可以是0人)的选法。

等式👉：先选正式代表，然后剩下n-m人分别有2种状态，选上或没选上

等式👈：这不是有正式代表和列席代表吗，直接用m+k表示，先从n人里面选m+k人，再从这m+k人里面选m个正式代表，然后根据k的取值范围做加法公式，就是思路。k的范围：。

看《具体数学》学到了新的符号：

$$r^{\underline k} = \frac{r!}{(r-k)!}$$