DES | Meta Field

0x00写在前面

没有根基也许可以建一座小屋，但绝对不能造一座坚固的大厦

0x01现代对称密码设计

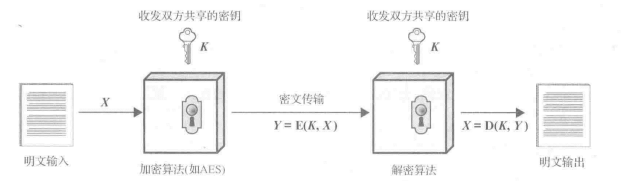
重点是对密钥的理解：密钥是加密算法的输入，但是独立于明文和算法。算法根据所用的特定的密钥产生不同的输出。算法使用的确切代替和变换也依赖于密钥。

对称密码首要的安全问题是：密钥的保密性。

0x02分组密码结构

分组密码是将明文分组作为整体加密，并且通常得到与明文等长的密文分组。典型的分组大小是64位或者128位。分组密码属于对称密码体制。

与分组密码相对应的还有流密码，但是流密码的应用远没有分组密码广泛，绝大部分基于网络的对称密码应用的是分组密码。

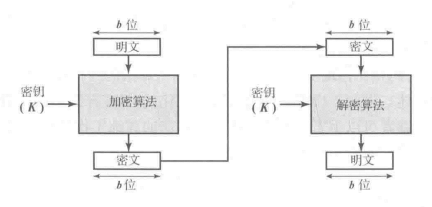
数学描述：

①将明文消息编码表示后的序列：$x0,x_1,\dots,x_i,\dots 划分成长为n位的组 (x_0,x_1,\dots,x{n-1})$ （长为n的矢量）

②各组分别在密钥空间 $K=(k0,k_1,\dots,k{t-1}) $的控制下变换为输出序列$ (y0,y_1,\dots,y{m-1})$。（长为m的矢量）

③加密算法

若，则称为拓展；若，则称为压缩

通常我们取，在二元情况下，明文和密文均是二元数字序列，他们的每个分量。

👉：有限域，，有限域的元素个数是一个素数的幂，是正整数，一般记为，我们最关注的只有两种情况：和。

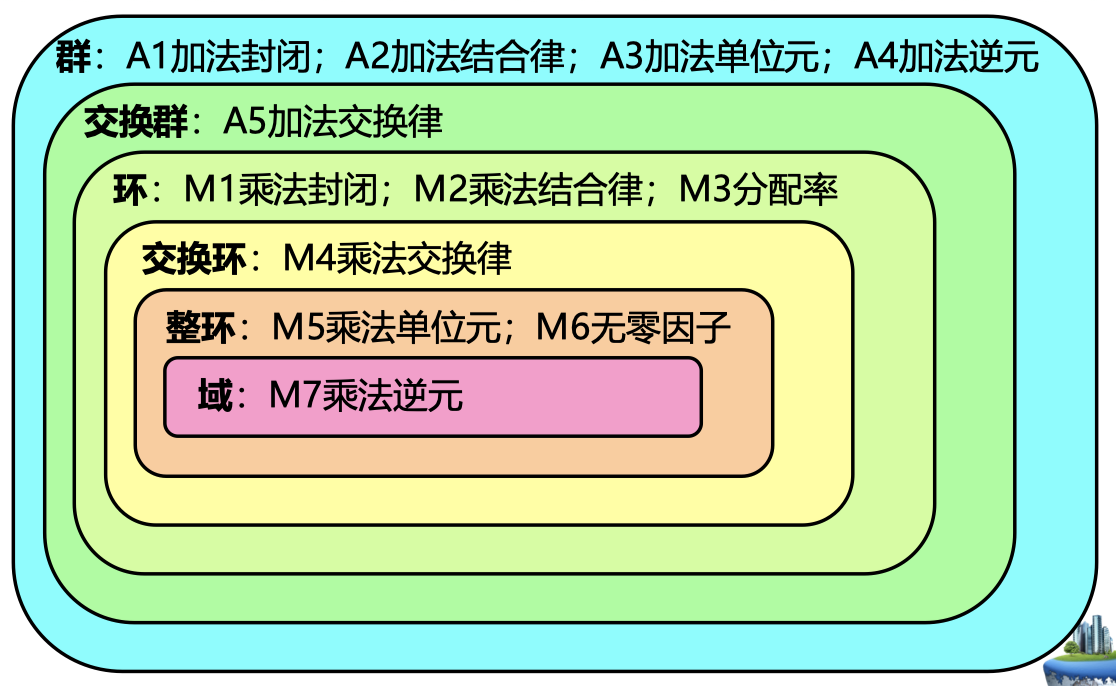
✍特点：同一密钥、加密算法，分组加密，分组长度固定

1945年，提出了设计密码体制的两种基本方法——混淆、扩散。

👋混淆：使密文与密钥之间的关系变得复杂。eg:DES中的S盒，其映射关系是精心设计以对抗攻击的。

👋扩散：密钥或明文的一个位变化要引起密文许多位的变化；密文每个位受多个明文位影响，可以使明文的统计特征消散在密文中，也可以引起雪崩效应（明文一个位变化引起密文多个位变化，且变化位未知）。对扩散的实现，一般采用线性变换、置换、循环移位等手段。

0x03Feistel密码结构

首先，记住这样一个事实：基于1945年的理论的密码结构仍然是当前使用的大多数重要对称分组密码的基本结构。

密码建议使用乘积密码的概念来逼近理想分组密码。

乘积密码：依次使用两个或两个以上基本密码进行多次迭代，所得结果的密码强度将强于所有单个密码的强度。多次迭代可以大大增强混淆和扩散的强度，使密文、明文、密钥之间的关系异常复杂，以至于攻击者极其难以分析。

数学描述：

和是两个密码体制，他们的明文空间和密文空间相同，设，那么和的乘积密码体制定义为，密钥形式为。

乘积密码通过交替使用代替(Substitution)和置换(Permutation)来实现混淆和扩散：

👋代替：每个明文元素或元素组被唯一替换为相应的密文元素或元素组。

👋置换：明文元素的序列被替换为该序列的一个置换。（置换：序列中元素出现的顺序改变，没有元素的增减）

结构的具体实现依赖于一下参数和特征：

✍分组长度：分组越长安全性越高，但是会降低加、解密的速度。传统上64位比较合理，高级加密标准用128位。

✍密钥长度：密钥越长安全性越高，但是会降低加、解密的速度。现在一般认为64位密钥不够，通常使用128位。

✍迭代轮数：密码的本质在于：单轮不能提供足够的安全性而多轮加密可以获得很高的安全性，迭代轮数典型值是16。

✍子密钥产生算法：产生越复杂，密码分析越难。

✍轮函数：越复杂抗攻击越强。

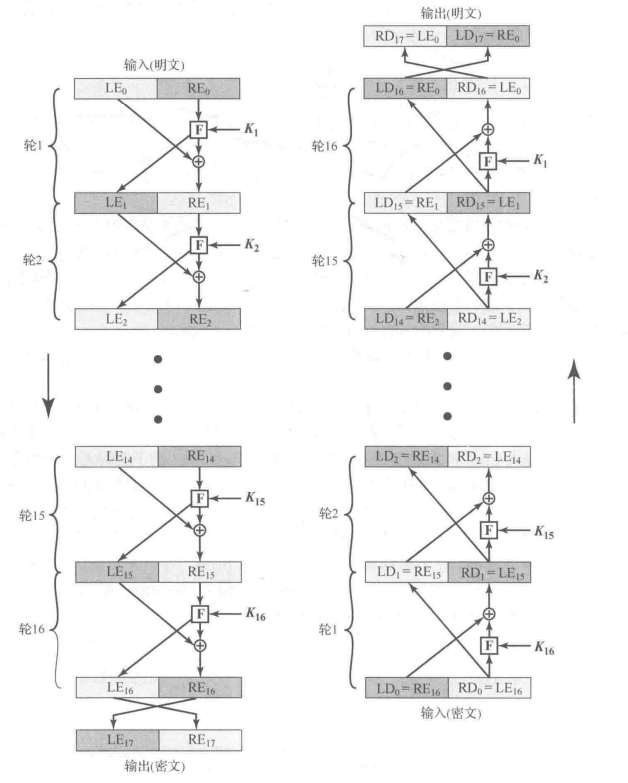
0x04DES算法

(Ⅰ)总览

DES(Data Encryption Standard)是在密码的基础上执行的，下面是DES的流程图：

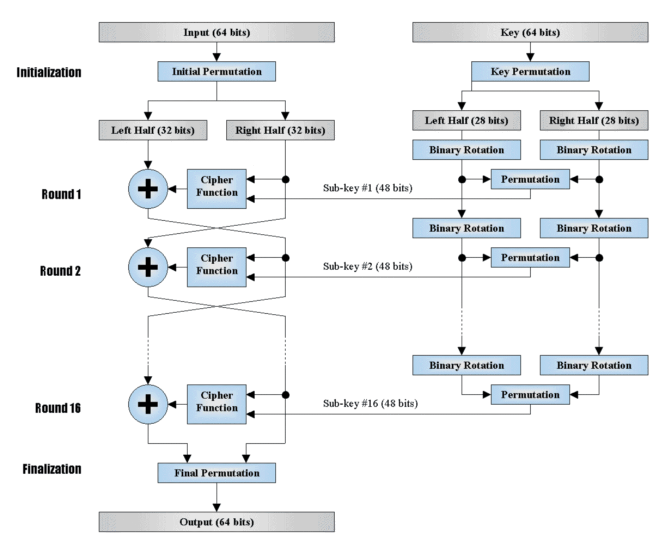
DES算法分为两大部分：迭代加密（左侧16轮迭代操作）、密钥调度（右侧生成子密钥的算法）。

密钥调度：从一把64-bit的主钥匙得到16把48-bit的子钥匙，然后把这些子钥匙用于迭代加密。

得到子钥匙：

1.从64-bit的主钥匙选特定的56位，其余位没有用，将这56位分成左右两个半密钥，都是28-bit的数组。

2.左右两个半密钥都循环左移一定位数，有些轮是1位，有些是2位。

3.把左右半密钥拼起来，再做一次置换，就得到了这一轮生成的子密钥。这个置换是从56-bit的数组里面选取指定的48位。所以每一轮都可以生成一个48位的子密钥。

4.重复2、3共16次即可。

迭代加密：

1.输入64位明文（长度为64位的布尔数组）做IP置换，仍然是64-bit数组

2.拆成左右各32位

3.每一轮迭代，都是接收一组，返回然后做下一轮迭代，数学描述：

$L' = R \\ R' = L \oplus F(R,subkey)$

其中函数也就是轮函数是整个算法的核心，作用：用一个子密钥加密32-bit的信息。

4.用之前的16个子密钥执行步骤3共16次

5.将步骤4得到的和拼接，做一次FP置换，得到密文。

DES算法加密解密过程几乎一致，唯一不同的是解密时子密钥使用顺序，是和加密过程使用子密钥相反的。

注✍IP 和 FP 其实只是一个标准而已，与安全性完全无关，因为 IP 和 FP 是完全公开的，大家都能做，所以这个步骤其实大可删了。比如 SM4 其实就没有这一步。

(Ⅱ)编码与加密

编码(encode)与加密(encrypt)都是把一条数据变成另一条数据的函数，但是有本质上的区别：

编码是公开的，是双向函数，比如：base64编码等

加密是私密的，必须有密钥才能加密或解密。

(Ⅲ)密钥调度算法

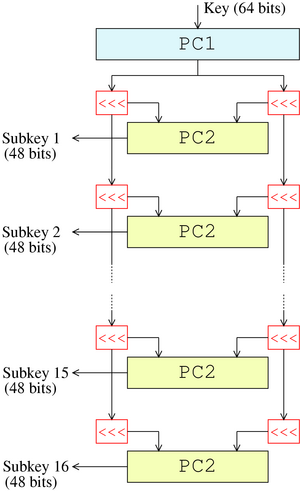
首先，是PC1置换，从64bit选出56位，这一步是，对安全没有帮助，代码实现如下：

# PC1，输入key，长度为64位的 0/1数组
# 从64位输入密钥中选择56位，分为左右两个28位的半密钥
def PC1(key):
    pc1_l = [57, 49, 41, 33, 25, 17, 9, 
            1, 58, 50, 42, 34, 26, 18, 
            10, 2, 59, 51, 43, 35, 27, 
            19, 11, 3, 60, 52, 44, 36]
    pc1_r = [63, 55, 47, 39, 31, 23, 15, 
            7, 62, 54, 46, 38, 30, 22, 
            14, 6, 61, 53, 45, 37, 29, 
            21, 13, 5, 28, 20, 12, 4]
    
    return [key[x-1] for x in pc1_l],[key[x-1] for x in pc1_r]

现在我们有两个28位的半密钥了，下面我们每一轮要把左、右半密钥循环左移，然后调用PC2方法来制造子密钥，框架如下：

def KeyGen(key):
    assert len(key) == 64
    l,r = PC1(key)
    off = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
    res = []

    for x in range(16):
        l = leftRotate(l,off[x])
        r = leftRotate(r,off[x])
        res.append(PC2(l+r))

    return res

leftRotate是循环左移：

def leftRotate(a,off):
    return a[off:] + a[:off]

assert leftRotate([0,1,0,1,1],2) == [0,1,1,0,1]

PC2是置换，将从左右半密钥拼起来的56位密钥中选48位作为一个子密钥：

# PC2，输入56位的Key
# 从56位的密钥中选取48位子密钥
def PC2(key):
    assert len(key) == 56
    pc2 = [14, 17, 11, 24, 1, 5, 
            3, 28, 15, 6, 21, 10,
            23, 19, 12, 4, 26, 8,
            16, 7, 27, 20, 13, 2,
            41, 52, 31, 37, 47, 55,
            30, 40, 51, 45, 33, 48,
            44, 49, 39, 56, 34, 53,
            46, 42, 50, 36, 29, 32]
    return [key[x-1] for x in pc2]

✍补充python中的assert（断言）:

写python代码使用assert是一个好习惯，用于判断一个表达式，在表达式条件为 false的时候触发异常，条件为true时正常执行后面的代码。

语法如下：

assert exp 
#等价于
if not exp:
	raise AssertionError

含有参数的情况：

assert exp [, arguments]
#等价于
if not exp:
	raise AssertionError(arguments)

到现在，我们就完成了密钥调度的部分。

(Ⅳ)加密迭代

首先，把明文进行IP置换，下一步进行16轮迭代，然后得到R+L并FP置换，输出密文，框架如下：

def DES(plain,key,method):
    subkeys =KeyGen(int2bin(key,64)) #生成子密钥
    
    if method == 'decrypt':
        subkeys = subkeys[::-1]
    
    m = IP(int2bin(plain,64)) #明文转二进制再IP置换
    l,r = np.array(m,dtype=int).reshape(2,-1).tolist()
    for i in range(16):
        l,r = goRound(l,r,subkeys[i])#使用本轮子密钥加密

    return bin2int(FP(r+l))

对于IP和FP这两个置换函数，这二者只是简单置换，对于安全没有任何意义，只是历史遗留原因，规定如下：

# 初始置换
def IP(a):
    ip = [58, 50, 42, 34, 26, 18, 10, 2,
            60, 52, 44, 36, 28, 20, 12, 4,
            62, 54, 46, 38, 30, 22, 14, 6,
            64, 56, 48, 40, 32, 24, 16, 8,
            57, 49, 41, 33, 25, 17, 9, 1,
            59, 51, 43, 35, 27, 19, 11, 3,
            61, 53, 45, 37, 29, 21, 13, 5,
            63, 55, 47, 39, 31, 23, 15, 7]
    return [a[x-1] for x in ip]

testM = [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1]

assert IP(testM) == [1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0]

# 最终置换
def FP(a):
    fp = [40, 8, 48, 16, 56, 24, 64, 32,
            39, 7, 47, 15, 55, 23, 63, 31,
            38, 6, 46, 14, 54, 22, 62, 30,
            37, 5, 45, 13, 53, 21, 61, 29,
            36, 4, 44, 12, 52, 20, 60, 28,
            35, 3, 43, 11, 51, 19, 59, 27,
            34, 2, 42, 10, 50, 18, 58, 26,
            33, 1, 41, 9, 49, 17, 57, 25]
    return [a[x-1] for x in fp]

✍注意：FP就是IP的逆函数

对于goRound每一轮要做的事情，我们知道是：

$L’ = R\\ R' = L \oplus F(R,subkey)$

1 2	def goRound(l,r,subKey): return r , binXor(l,Feistel(r,subKey))

对于Feitel函数（轮函数）：

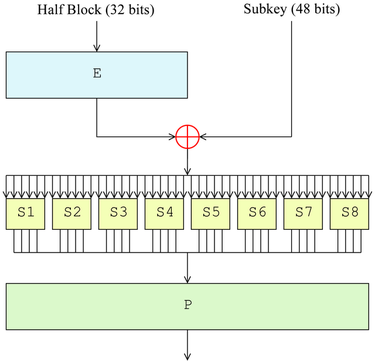
轮函数本质是一个PRF（伪随机函数），它的目的就是根据输入生成一个随机程度很高的比特串，将这个比特串异或到另一个比特串上就实现了加密。

轮函数有4个过程：明文扩展、轮密钥异或、S 盒和 P 盒。

一个32bit的块，经过Expand函数变成48位，然后与子密钥异或，得到的48位结果分为8组，每一组是6位，丢进对应的S盒，输出4bit的信息，把这些信息收集起来一共是32位，做一次P置换，得到此轮32bit的结果：

def Feistel(a, subKey):
    assert len(a) == 32
    assert len(subKey) == 48

    t = binXor(Expand(a), subKey)
    t = S(t)
    t = P(t)

    return t

Expand 算法是指定的：

# 扩张置换，将32位的数据扩展到48位
def Expand(a):
    assert len(a) == 32
    e = [32, 1, 2, 3, 4, 5,
        4, 5, 6, 7, 8, 9,
        8, 9, 10, 11, 12, 13,
        12, 13, 14, 15, 16, 17,
        16, 17, 18, 19, 20, 21,
        20, 21, 22, 23, 24, 25,
        24, 25, 26, 27, 28, 29,
        28, 29, 30, 31, 32, 1]
    return [a[x-1] for x in e]

P置换：

# P置换
def P(a):
    assert len(a) == 32

    p = [16, 7, 20, 21,
        29, 12, 28, 17,
        1, 15, 23, 26,
        5, 18, 31, 10,
        2, 8, 24, 14,
        32, 27, 3, 9,
        19, 13, 30, 6,
        22, 11, 4, 25]
    return [a[x-1] for x in p]

S盒：在分组密码结构中，是唯一的非线性结构，一共有8张表，我们之前分完的8组分别使用来进行变换，代码实现如下：

# S盒变换，输入48位，输出32位
def S(a):
    assert len(a) == 48

    S_box = [[14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
                0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
                4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
                15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13], 
                [15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
                3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
                0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
                13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9], 
                [10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
                13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
                13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
                1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12],
                [7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
                13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
                10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
                3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14],
                [2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
                14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
                4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
                11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3],
                [12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
                10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
                9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
                4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13],
                [4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
                13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
                1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
                6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12],
                [13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
                1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
                7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
                2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11]]

    a = np.array(a, dtype=int).reshape(8, 6)
    res = []

    for i in range(8):
        # 用 S_box[i] 处理6位a[i]，得到4位输出
        p = a[i]
        r = S_box[i][bin2int([p[0], p[5], p[1], p[2], p[3], p[4]])]
        res.append(int2bin(r, 4))
        
    res = np.array(res).flatten().tolist()
    assert len(res) == 32

    return res

(Ⅴ)完整加密解密代码

from functools import reduce
import numpy as np

# 整数转二进制数组，指定位长 n，大端序
def int2bin(a, n):
    assert 0<=n and a < 2**n
    res = np.zeros(n, dtype = int)

    for x in range(n):
        res[n-x-1] = a % 2
        a = a // 2
    return res.tolist()

assert int2bin(0x1a, 10) == [0, 0, 0, 0, 0, 1, 1, 0, 1, 0]

# 二进制数组转整数，大端序
def bin2int(a):
    return reduce(lambda x,y: x*2+y, a)

assert bin2int([0, 0, 0, 0, 0, 1, 1, 0, 1, 0]) == 0x1a

# 循环左移off位
def leftRotate(a, off):
    return a[off:] + a[:off]

assert leftRotate([0, 1, 0, 1, 1], 2) == [0, 1, 1, 0, 1]

# 异或
def binXor(a, b):
    assert len(a) == len(b)
    return [x^y for x, y in zip(a, b)]
assert binXor([1, 1, 0, 1], [0, 1, 1, 0]) == [1, 0, 1, 1]

# 初始置换
def IP(a):
    ip = [58, 50, 42, 34, 26, 18, 10, 2,
            60, 52, 44, 36, 28, 20, 12, 4,
            62, 54, 46, 38, 30, 22, 14, 6,
            64, 56, 48, 40, 32, 24, 16, 8,
            57, 49, 41, 33, 25, 17, 9, 1,
            59, 51, 43, 35, 27, 19, 11, 3,
            61, 53, 45, 37, 29, 21, 13, 5,
            63, 55, 47, 39, 31, 23, 15, 7]
    return [a[x-1] for x in ip]
testM = [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1]
assert IP(testM) == [1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0]

# 最终置换
def FP(a):
    fp = [40, 8, 48, 16, 56, 24, 64, 32,
            39, 7, 47, 15, 55, 23, 63, 31,
            38, 6, 46, 14, 54, 22, 62, 30,
            37, 5, 45, 13, 53, 21, 61, 29,
            36, 4, 44, 12, 52, 20, 60, 28,
            35, 3, 43, 11, 51, 19, 59, 27,
            34, 2, 42, 10, 50, 18, 58, 26,
            33, 1, 41, 9, 49, 17, 57, 25]
    return [a[x-1] for x in fp]
    
# 选择置换1
# 从64位输入密钥中选择56位，分为左右两个28位半密钥
def PC1(key):
    pc1_l = [57, 49, 41, 33, 25, 17, 9, 
            1, 58, 50, 42, 34, 26, 18, 
            10, 2, 59, 51, 43, 35, 27, 
            19, 11, 3, 60, 52, 44, 36]
    pc1_r = [63, 55, 47, 39, 31, 23, 15, 
            7, 62, 54, 46, 38, 30, 22, 
            14, 6, 61, 53, 45, 37, 29, 
            21, 13, 5, 28, 20, 12, 4]
    
    return [key[x-1] for x in pc1_l], [key[x-1] for x in pc1_r]

testKey = [0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1]
testL, testR = PC1(testKey)
assert testL + testR == [1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1]

# 选择置换2
# 从56位的密钥中选取48位子密钥
def PC2(key):
    assert len(key) == 56

    pc2 = [14, 17, 11, 24, 1, 5, 
            3, 28, 15, 6, 21, 10,
            23, 19, 12, 4, 26, 8,
            16, 7, 27, 20, 13, 2,
            41, 52, 31, 37, 47, 55,
            30, 40, 51, 45, 33, 48,
            44, 49, 39, 56, 34, 53,
            46, 42, 50, 36, 29, 32]
    return [key[x-1] for x in pc2]

# 子密钥生成算法，由一个64位主密钥导出16个48位子密钥
def keyGen(key):
    assert len(key) == 64

    l, r = PC1(key)
    off = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
    res = []

    for x in range(16):
        l = leftRotate(l, off[x])
        r = leftRotate(r, off[x])

        res.append(PC2(l + r))
    
    return res

assert keyGen(testKey)[-1] == [1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1]

# S盒变换，输入48位，输出32位
def S(a):
    assert len(a) == 48

    S_box = [[14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
                0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
                4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
                15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13], 
                [15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
                3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
                0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
                13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9], 
                [10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
                13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
                13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
                1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12],
                [7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
                13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
                10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
                3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14],
                [2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
                14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
                4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
                11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3],
                [12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
                10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
                9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
                4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13],
                [4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
                13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
                1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
                6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12],
                [13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
                1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
                7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
                2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11]]

    a = np.array(a, dtype=int).reshape(8, 6)
    res = []

    for i in range(8):
        # 用 S_box[i] 处理6位a[i]，得到4位输出
        p = a[i]
        r = S_box[i][bin2int([p[0], p[5], p[1], p[2], p[3], p[4]])]
        res.append(int2bin(r, 4))
        
    res = np.array(res).flatten().tolist()
    assert len(res) == 32

    return res

# 扩张置换，将32位的半块扩展到48位
def Expand(a):
    assert len(a) == 32
    e = [32, 1, 2, 3, 4, 5,
        4, 5, 6, 7, 8, 9,
        8, 9, 10, 11, 12, 13,
        12, 13, 14, 15, 16, 17,
        16, 17, 18, 19, 20, 21,
        20, 21, 22, 23, 24, 25,
        24, 25, 26, 27, 28, 29,
        28, 29, 30, 31, 32, 1]
    return [a[x-1] for x in e]

# P置换
def P(a):
    assert len(a) == 32

    p = [16, 7, 20, 21,
        29, 12, 28, 17,
        1, 15, 23, 26,
        5, 18, 31, 10,
        2, 8, 24, 14,
        32, 27, 3, 9,
        19, 13, 30, 6,
        22, 11, 4, 25]
    return [a[x-1] for x in p]

# F函数，用于处理一个半块
def Feistel(a, subKey):
    assert len(a) == 32
    assert len(subKey) == 48

    t = binXor(Expand(a), subKey)
    t = S(t)
    t = P(t)

    return t

def goRound(l, r, subKey):
    return r, binXor(l, Feistel(r, subKey))

def DES(plain, key, method):
    subkeys = keyGen(int2bin(key, 64))

    if method == 'decrypt':
        subkeys = subkeys[::-1]
    
    m = IP(int2bin(plain, 64))

    l, r = np.array(m, dtype=int).reshape(2, -1).tolist()

    for i in range(16):
        l, r = goRound(l, r, subkeys[i])
    
    return bin2int(FP(r + l))

print(hex(DES(0x11aabbccddeeff01, 0xcafababedeadbeaf, 'encrypt')))
# 0x2973a7e54ec730a3
print(hex(DES(0x2973a7e54ec730a3, 0xcafababedeadbeaf, 'decrypt')))
# 0x11aabbccddeeff01

0x05DES差分攻击

(Ⅰ)总览

数学中把一个数列相邻两个数之间做差，得到的新数列就叫差分数列。

密码学中的差分运算实质上是两个01比特串之间做异或操作。

DES的核心是函数：

函数保密作用就在子密钥异或这一步，此时聪明的密码学家们就注意到，两个明文的差分和用同一个密钥异或后的差分是一样的。因为异或有如下性质：

$(X\oplus Y)\oplus Y = X \\ X \oplus Y = Y \oplus X$

于是我们可以绕过密钥随机性的影响，直接得到S盒的差分，但是要注意：差分攻击是选择明文攻击，也就是要用待破解的算法加密任意字节，并得到加密结果，才能实现攻击。

(Ⅱ)差分密码分析

差分密码分析()使用固定差异相关的明文对()，对于差分有很多定义方式，其中使用异或()是最常见的。

最基本的差分密码分析密钥破解形式中，攻击者首先获取大量明文对的密文，并假设差分在至少轮后有效，即加密算法的总轮数。攻击者在倒数第二轮与最后一轮之间差异固定的假设下，去推测可能的轮密钥。如果轮密钥比较短，那么只需举可能的轮密钥，直到最后一轮运算结果和差异的密文对一致即可。当一个轮密钥看起来明显比其他密钥常出现时，其会被假设是正确的轮密钥。

自从差分密码分析进入公众视野，其就成了加密设计者的基本考量。新的加密设计通常需要举证其算法可以抗此类攻击。包括AES在内的许多算法都被证明在差分分析攻击下是安全的。

(Ⅲ)攻击细则

攻击主要依赖于一点：给定输入/输出，差异特征仅在特定输入下出现。这种方法通常用于线性结构组成的加密方式，如S盒。给定两个已知密文或明文后，观察其输出差异可猜测密钥的可能值。

(Ⅳ)差分攻击一些定义

①差分值(difference)

设 $X,X^ \in {0,1}^n $，则$ X $和$ X^ $的差分值定义为$ \Delta X=X \oplus X^*$

②差分对(differential)

设，假设迭代分组密码的输入对 $(X,X^) $的差分值为$ X \oplus X^ = \alpha $，经过$ i $轮加密后，输出对$ (Y_i,Y_i^) $的差分值为$ Y_i \oplus Y_i^= \beta $，则称$ (\alpha,\beta) $为该密码的一个$ i $轮差分对。特别地，当$ i=1 $时，$ (\alpha,\beta) $显示了轮函数的差分传播特性，称$ \alpha $为$ F $的输入差分，$ \beta $为$ F$的输出差分。

③差分特征

迭代分组密码的一条轮差分特征是指：当输入对$(X,X^) $的满足$ X \oplus X^ = \beta_0 $时，$ i $轮加密的中间状态$ (Y_j,Y_j^) $满足$ Y_j \oplus Y_j^ = \beta_j $，其中$ j=1,2,\dots,i$。

差分特征也称差分路径，它与差分对的区别在于差分对只规定了输入和输出差分，而差分路径则指定了中间状态的差分值。

④差分概率

迭代分组密码的一条轮差分所对应的概率是指：在输入、每轮子密钥取值独立且均匀分布的情况下，差分对为的概率。特别地，当时，表示轮函数的差分传播概率。

⑤差分特征概率

迭代分组密码的一条轮差分特征的概率是指在输入、轮密钥取值独立且均匀分布的情况下，差分特征为的概率。

当时，差分概率和差分特征概率存在这样的关系：

$DP(\Omega) = \prod_{j=1}^{i} DP(\beta_{j-1}, \beta_j)$

⑥正确对与错误对

给定一条差分特征，若输入对 $(X, X^)$ 在加密过程中的中间状态的差分满足差分特征 ，则称 $(X, X^) $对于$ \Omega$ 是一个正确对，否则是错误对。在输入对和轮密钥随机且均匀选取的情况下，输入对是正确对的概率就是。

⑦差分区别器

对于上的一个随机置换，给定任意非零差分对，则。

如果找到了一条轮差分，其概率大于，就可以将轮的加密算法与随机置换区分开。这种差分就叫做差分区别器。

⑧异或运算的差分性质

假设，则:

$\Delta z = \Delta (x \oplus y) = (x\oplus y)\oplus (x^ \oplus y^)=(x \oplus x^) \oplus (y \oplus y^)=\Delta x \oplus \Delta y$

注👋差分密码相关英文文献中，和是两个不同的概念：是差分值，是差分对；但是在中文文献中二者都被翻译为差分，要根据具体的语境自行体会。

(Ⅴ)S盒差分攻击模型

DES 能够使用差分攻击的原因在于 S 盒的差分分布具有不均匀性。也就是说对于相同的输入差分，不同的输入对应着不同的输出差分（👋注意区分输入和输入差分）。

为明文输入，为密钥，是盒的输入，是密文。

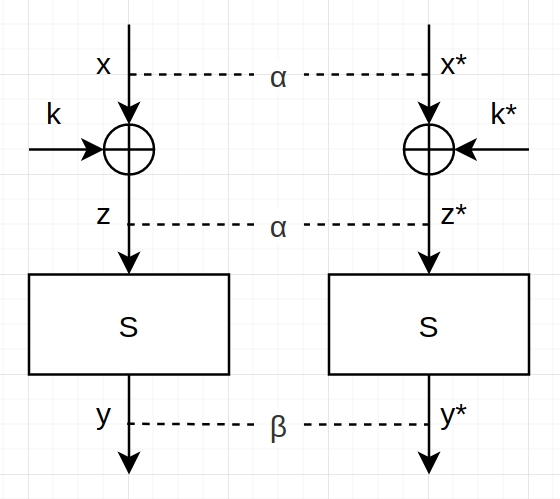
我们记输入差分为，输出差分为，那么定义

$IN_s(\alpha,\beta)=\{x \in \{ 0,1 \}^8 | S(x \oplus \alpha) \oplus S(x)=\beta \} \\ N_s(\alpha,\beta) = \# IN_s(\alpha,\beta)$

其中表示的是的个数，我们称之为S盒的差分分布表；直接理解为全体长度为8的01bit串的集合。

我们随意选取一个输入差分，一对输入，并得到输出差分，求出就可以知道经过密钥异或后的输入的取值范围。这个集合一般是的真子集，因此排除了一些不可能的密钥。重复选取多对和，最后就可以将范围缩小至一个密钥，到此成功破解。

(Ⅵ)5轮DES差分攻击分析

需要选取合适的输入差分，就有办法求出最后一个 S 盒的输出差分。

注👋此处的差分是结构里的，而不是DES整个结构的差分。

现在取差分对作为结构的输入差分，可以得到如下的差分传播路径：

其中：

表示轮函数输入差分

表示轮函数输出差分

是函数的输入差分和输出差分

表示该字节差分未知，表示这个字节的差分值就是

我们看到，输入差分仅有 1 个比特为 1 ，在第 3 轮时差异还没有完全扩散开。只需要对第 3 轮函数的输出做逆 P 盒，就可以得到一个第 1 和第 7 字节都是 0 的比特串。

$P^{-1}(C') = P^{-1}(P(0*****0*_{x}))=0*****0*_{x}$

下面是DES差分攻击最精彩的地方，我们写出最后一轮函数的输出：

$l' = E' \oplus d' \\ l'\oplus d' = E' \oplus d' \oplus d' \\ l'\oplus d' = E'$

展开：

$E' = l'\oplus d' = l' \oplus L' \oplus A' \oplus C'$

由于 P 盒也是一个一一置换，所以如果 P 盒的输入差分为 0 （输入没有区别），那么输出差分也为 0 （输出也没有区别）。那么有。所以有：

$E' = l' \oplus L' \oplus C' = l' \oplus 20000000_x \oplus P(0*****0*_x)$

然后我们对做逆P盒置换就得到了S盒的输出差分，流程图如下：

1 2	graph LR A[S-box] -->\|S-box输出差分\| B[P-box] -->\|得到\| C[E']

对于P盒，它仅仅替换字节的顺序，有的性质，于是有：

$P^{-1}(E') = P^{-1}(l' \oplus 20000000_x \oplus P(0*****0*_x)) \\ \qquad \qquad \qquad \ = P^{-1}(l' \oplus 20000000_x) \oplus P^{-1}(P(0*****0*_x)) \\ \qquad \,= P^{-1}(l' \oplus 20000000_x) \oplus 0*****0*_x \\$

到此，我们求出了第1个和第7个S盒的输出差分；S盒的输入差分就是，知道输入差分和输出差分，就可以还原最后一轮密钥的第1和第7部分，密钥共12bit，剩下部分选择其它差分路径。

0x06python代码细节补充

reduce()

在 python 2 是内置函数，从python 3 开始移到了 functools 模块。

reduce的工作过程是：在迭代序列的过程中，首先把 前两个元素（只能两个）传给函数，函数加工后，然后把 得到的结果和第三个元素 作为两个参数传给函数参数， 函数加工后得到的结果又和第四个元素 作为两个参数传给函数参数，依次类推。

reduce(function, iterable[, initializer])
#function：函数
#iterable：序列
#initializer：初始值（可选）

举例1：阶乘

>>> def mul(x, y):
...     return x*y
...
>>> from functools import reduce
>>> reduce(mul, [1,2,3,4])
10
>>>

举例2：整数列表整数

>>> from functools import reduce
>>> reduce(lambda x, y: x * 10 + y, [1 , 2, 3, 4, 5])
12345
>>>

flatten()

只适用于numpy对象，即array或mat；

默认缺省参数为0；

数组降维：默认按照行的方向降维到一维

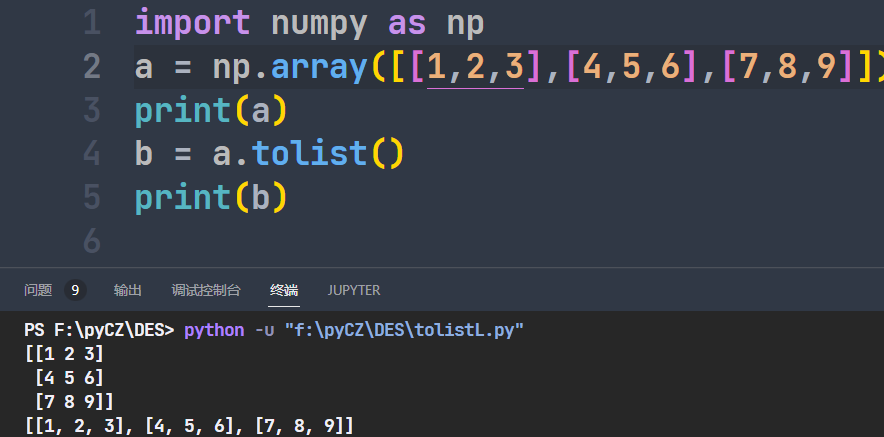
tolist()

数组转换为列表

0x07实验感想

通过本次DES实验，我深刻理解了DES加解密的过程与细节，同时通过对密码差分攻击的深入学习，也适当锻炼了数学思维，拓展了其它方面的知识如：离散数学中域的概念、python的一些库函数、异或运算的性质、typora绘制流程图等，同时也意识到向更优秀的学长们学习的必要性，这次实验对我是一次很好的锻炼与成长。

0x08参考资料

1.阮师傅的Blog

2.cdcq的Blog

（阮师傅的博客和cdcq学长的博客写的非常好，我就是根据他们的文章进行学习的）

3.《密码编码学与网络安全——原理与实践（第八版）》William Stallings著电子工业出版社

4.《分组密码的攻击方法与实例分析》李超孙兵李瑞林著科学出版社

5.《Python密码学编程（第二版）》Al Sweigart著人民邮电出版社

6.Wiki-pedia:Data Encryption Standard

0x09 DES C语言版

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#pragma warning(disable:4996)
#define MAX 100
using namespace std;
//程序说明：
//
//1、输入的明文长度大于0即可，明文可以带空格；
//
//2、输入的明文支持汉字；
//
//3、输出密文默认为二进制字符串；
//
//4、输入密文要求为二进制字符串且长度为64的倍数，否则解密会出错。

//模式标记,确定是加密还是解密
int flag;
string k[16];
//PC-1选位表
int pc1Table[56] = {
	57,49,41,33,25,17,9,1,
	58,50,42,34,26,18,10,2,
	59,51,43,35,27,19,11,3,
	60,52,44,36,63,55,47,39,
	31,23,15,7,62,54,46,38,
	30,22,14,6,61,53,45,37,
	29,21,13,5,28,20,12,4
};
//PC-2选位表
int pc2Table[48] =
{
	14,17,11,24,1,5,
	3,28,15,6,21,10,
	23,19,12,4,26,8,
	16,7,27,20,13,2,
	41,52,31,37,47,55,
	30,40,51,45,33,48,
	44,49,39,56,34,53,
	46,42,50,36,29,32
};
//左移位数表
int loopTable[16] =
{
	1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1
};
//IP表（初始置换表）
int ipTable[64] =
{
	58,50,42,34,26,18,10,2,
	60,52,44,36,28,20,12,4,
	62,54,46,38,30,22,14,6,
	64,56,48,40,32,24,16,8,
	57,49,41,33,25,17,9,1,
	59,51,43,35,27,19,11,3,
	61,53,45,37,29,21,13,5,
	63,55,47,39,31,23,15,7
};
//逆置换IP^-1表(解密时IP初始置换的逆)
int ipReverseTable[64] = {
	40,8,48,16,56,24,64,32,
	39,7,47,15,55,23,63,31,
	38,6,46,14,54,22,62,30,
	37,5,45,13,53,21,61,29,
	36,4,44,12,52,20,60,28,
	35,3,43,11,51,19,59,27,
	34,2,42,10,50,18,58,26,
	33,1,41,9,49,17,57,25
};
//扩展置换表(E盒)
int extendTable[48] =
{
	32,1,2,3,4,5,
	4,5,6,7,8,9,
	8,9,10,11,12,13,
	12,13,14,15,16,17,
	16,17,18,19,20,21,
	20,21,22,23,24,25,
	24,25,26,27,28,29,
	28,29,30,31,32,1
};

//八个S盒，三维数组存储
int sBox[8][4][16] =
{
	//S1
	14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
	0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
	4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
	15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13,
	//S2
	15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
	3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
	0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
	13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9,
	//S3
	10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
	13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
	13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
	1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12,
	//S4
	7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
	13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
	10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
	3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14,
	//S5
	2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
	14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
	4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
	11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3,
	//S6
	12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
	10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
	9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
	4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13,
	//S7
	4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
	13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
	1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
	6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12,
	//S8
	13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
	1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
	7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
	2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11
};

//置换表(P盒)
int pTable[32] =
{
	16,7,20,21,
	29,12,28,17,
	1,15,23,26,
	5,18,31,10,
	2,8,24,14,
	32,27,3,9,
	19,13,30,6,
	22,11,4,25
};
//字符转二进制，会有些怪异，但是后面用binaryToInt函数解决
string charToBinary(char c)
{
	int i, b = c, k = 0, flag = 0;
	string result;
	//负数就是中文字符
	if (b < 0)
	{
		b = -b;
		flag = 1;
	}
	//英文字符转换成ASCII的倒序！！！所以最后需要逆序
	while (k < 8)
	{
		if (b)
		{
			//转换成字符型的 ‘1’或‘0’
			result += ((b % 2) + '0');
			b /= 2;
		}
		else result += '0';
		k++;
	}
	//汉字字符处理，汉字用两个char类型处理，用来表示汉字的任何其中一个char都是负数，要从int型数据，将其恢复成原本的存储形式（补码）
	if (flag)
	{
		for (i = 0; i < result.length(); i++)
		{
			//'0'->'1','1'->'0'
			if (result[i] == '0') result[i] = '1';
			else result[i] = '0';
		}
		for (i = 0; result[i] != '0'; i++)
		{
			result[i] = '0';
		}
		result[i] = '1';
	}
	reverse(result.begin(), result.end());   //中文字符最后变成了补码，英文字符正常的ASCII码
	return result;
}
//二进制转整型
int binaryToInt(string s)
{
	int i, result = 0, p = 1;
	for (i = s.length() - 1; i >= 0; i--)
	{
		result += ((s[i] - '0') * p);
		p *= 2;
	}
	return result;
}
//整型转二进制，用来将进入S盒后取出的数据转化为二进制，最多用4bit(while循环中4的出处)
string intToBinary(int i)
{
	int k = 0;
	string result;
	while (k < 4)
	{
		if (i)
		{
			result += ((i % 2) + '0');
			i /= 2;
		}
		else result += '0';
		k++;
	}
	reverse(result.begin(), result.end());
	return result;
}
//异或运算
string xorAB(string a, string b)
{
	int i;
	string result;
	//按位异或运算
	for (i = 0; i < a.length(); i++)
	{
		result += (((a[i] - '0') ^ (b[i] - '0')) + '0');
	}
	return result;
}
//f函数
string f(string right, string k)  //right明文当前加密轮右侧比特流，k当前加密轮密钥
{
	int i, temp;
	string extendBinary, b0;
	string b[8], row, col;
	string b8, pb;
	//extendBinary用来存放右侧32明文经过E盒扩展后的内容
	for (i = 0; i < 48; i++)
	{
		extendBinary += right[extendTable[i] - 1];//E盒从一开始，所以要减一
	}
	//扩展后的内容与此轮密钥异或操作并将结果存入b0中
	b0 = xorAB(extendBinary, k);
	//将b0的内容分成八份，每份六bit，为进入S盒做准备
	for (i = 0; i < 8; i++)
	{
		b[i] = b0.substr(i * 6, 6);
	}

	for (i = 0; i < 8; i++)
	{   //6bit的第一位和第六位作为行坐标
		row = b[i].substr(0, 1) + b[i].substr(5, 1);
		//6bit的第二至五位作为纵坐标
		col = b[i].substr(1, 4);
		//转化为整形坐标后，第几份对应去找第几个S盒替换
		temp = sBox[i][binaryToInt(row)][binaryToInt(col)];
		//转到b8中合并
		b[i] = intToBinary(temp);
		b8 += b[i];
	}
	//进入置换盒(P盒)
	for (i = 0; i < 32; i++)
	{
		pb += b8[pTable[i] - 1];
	}
	//一轮加密结束，返回结果
	return pb;
}
//明文/密文处理,以明文处理过程为例进行解释
string wen(string wenBinary[], int num)
{
	int i, j;
	string ipWenBinary[100];
	string left[17], right[17], temp, result;
	//将明文初始置换，num表示分块数目
	for (i = 0; i < num; i++)
	{
		temp = "";
		for (j = 0; j < 64; j++)
		{
			temp += wenBinary[i][ipTable[j] - 1];
		}
		ipWenBinary[i] = temp;
	}
	for (i = 0; i < num; i++)
	{   //将初始置换后的每块明文拆成左右两部分
		left[0] = ipWenBinary[i].substr(0, 32);
		right[0] = ipWenBinary[i].substr(32, 32);

		//十六轮加密
		for (j = 0; j < 16; j++)
		{
			//左侧下一个等于当前右侧
			left[j + 1] = right[j];
			//加密和解密的区别，flag是那个全局变量

			//右侧下一个为:当前左侧与当前右侧走完一轮加密后的结果进行异或的结果
			if (flag == 1 || flag == 3) right[j + 1] = xorAB(left[j], f(right[j], k[j]));

			//倒着解密
			else right[j + 1] = xorAB(left[j], f(right[j], k[15 - j]));
		}
		//加密后的左右和在一起
		temp = right[j] + left[j];
		//将加密后的密文进行最后的置换，实际上和初始置换是对称的~！
		//每块的加密结果都和在result中,加密可以直接输出比特流
		for (j = 0; j < 64; j++)
		{
			result += temp[ipReverseTable[j] - 1];
		}
	}
	//解密结果输出的是字符
	if (flag == 2 || flag == 4)
	{
		string ch;
		for (i = 0; i < num * 8; i++)
		{
			//超过char类型的表示范围就是中文字符的一部分，强转为char类型
			ch += binaryToInt(result.substr(8 * i, 8));
		}
		result = ch;
	}
	return result;
}
//密钥处理
void miyao()
{
	int i, j;
	string miyao, miyaoBinary, pc1MiyaoBinary;
	string c[17], d[17], temp, pc2Temp;
	cout << "请输入密钥：";
	while (cin >> miyao)
	{
		if (miyao.length() < 9) break;
		else cout << "密钥不能超过8位，请重新输入：";
	}
	for (i = 0; i < miyao.length(); i++)
	{
		miyaoBinary += charToBinary(miyao[i]);
	}
	//密钥长度不足64bit，补‘0’
	while (miyaoBinary.length() % 64 != 0)
	{
		miyaoBinary += '0';
	}
	//从64bit密钥中依据PC-1盒子取出56bit
	for (i = 0; i < 56; i++)
	{
		pc1MiyaoBinary += miyaoBinary[pc1Table[i] - 1];
	}
	//56bit分成左右两部分
	c[0] = pc1MiyaoBinary.substr(0, 28);
	d[0] = pc1MiyaoBinary.substr(28, 28);
	//产生16轮加密需要的密钥，存入全局变量k[]中
	for (i = 1; i <= 16; i++)

	{   //根据循环移位表，确定生成该轮密钥移位数目       
		c[i] = c[i - 1].substr(loopTable[i - 1], 28 - loopTable[i - 1]) + c[i - 1].substr(0, loopTable[i - 1]);
		d[i] = d[i - 1].substr(loopTable[i - 1], 28 - loopTable[i - 1]) + d[i - 1].substr(0, loopTable[i - 1]);

		temp = c[i] + d[i];
		pc2Temp = "";
		//依据PC-2盒子进行操作
		for (j = 0; j < 48; j++)
		{
			pc2Temp += temp[pc2Table[j] - 1];
		}
		//生成该轮密钥
		k[i - 1] = pc2Temp;
	}
}


int main() {
	int i, num;
	string wenString, wenBinary[100], temp;
	while (1)
	{
		cout << "请选择模式：0:退出程序 1：加密文件 2：解密文件\n填写数字序号：";
		cin >> flag;
		if (!flag) break;
		else if ((flag != 1) && (flag != 2) )
		{
			cout << "输入不合法，请重新输入！" << endl << endl;
			continue;
		}
		num = 0;
		miyao();
		getchar();
		switch (flag)
		{
		case 1:
			wenString = "";
			char fname_P[MAX]; //存储需要加密文件的名字
			char fname_E[MAX];  //存储加密后文件的名字
			char cipher[100][65];   //存储加密后的密文
			FILE* fp_p;     //指向存储需要加密文件
			FILE* fp_e;     //指向加密后文件
			int ch;
			cout << "请输入要加密文件的名字(用绝对路径且路径名不包含空格):" << endl;
			cin >> fname_P;
			cout << "请输入加密后文件的名字(用绝对路径且路径名不包含空格):" << endl;
			cin >> fname_E;
			//打开需要加密的文件
			if ((fp_p = fopen(fname_P, "r")) == NULL) {
				printf("打开文件失败!\n");
			}
			//打开加密后文件内容被存储的位置
			if ((fp_e = fopen(fname_E, "w")) == NULL) {
				printf("打开文件失败!\n");
			}
			while ((ch = fgetc(fp_p)) != EOF) {
				wenString += ch;
			}
			for (i = 0; i < wenString.length(); i++)
			{
				temp += charToBinary(wenString[i]);
				//字符每满8bit为一组，最后一组可以不满8bit，后面会补0
				if (((i + 1) % 8 == 0) || (((i + 1) % 8 != 0) && (i == wenString.length() - 1)))
				{
					wenBinary[num++] = temp;
					temp = "";
				}
			}
			//最后一组不满64位就补零，补的零，一定是八的整数倍，二进制00000000为null空字符，不输出
			while (wenBinary[num - 1].length() % 64 != 0)
			{
				wenBinary[num - 1] += '0';
			}
			temp = wen(wenBinary, num);
			for (i = 0; i < num; i++) {
				//每64个字符放到一个数组中
				temp.copy(cipher[i], 64, 64 * i);
				//每个数组最后补全最后一位的'\0'，以便写入文件
				cipher[i][64] = '\0';
				//写入文件
				fputs(cipher[i], fp_e);
			}
			//关闭文件
			fclose(fp_e);
			fclose(fp_p);
			break;
		case 2:
			wenString = "";
			char fname_Cipher[MAX];  //存储需要解密文件的名字
			char fname_P1[MAX];       //存储解密后文件的名字
			char plaintext[1024];
			cout << "请输入要解密文件的名字(用绝对路径且路径名不包含空格)" << endl;;
			cin >> fname_Cipher;
			cout << "请输入解密后文件的名字(用绝对路径且路径名不包含空格)" << endl;;
			cin >> fname_P1;
			FILE* fp_cipher;    //指向需要解密的文件
			FILE* fp_p1;         //指向解密后的文件
			//打开需要解密的文件
			if ((fp_cipher = fopen(fname_Cipher, "r")) == NULL) {
				printf("打开文件失败!\n");
			}
			//打开解密后文件内容被存储的位置
			if ((fp_p1 = fopen(fname_P1, "w")) == NULL) {
				printf("打开文件失败!\n");
			}
			while ((ch = fgetc(fp_cipher)) != EOF) {
				wenString+= ch;
			}
			for (i = 0; i * 64 < wenString.length(); i++)
			{
				wenBinary[num++] = wenString.substr(i * 64, 64);
			}
			//将文件内容解密
			temp = wen(wenBinary, num);
			int n = temp.length();
			//将解密后字符放在一个数组中
			temp.copy(plaintext,n, 0);
			//补全最后一位的'\0'，以便写入文件
			plaintext[n] = '\0';
			fputs(plaintext, fp_p1);
			//关闭文件
			fclose(fp_cipher);
			fclose(fp_p1);
		}

	}
	return 0;
}