课程报告

后量子密码-格密码学

一.后量子密码

0x01 什么是后量子密码

后量子密码是能够抵抗量子计算机对现有密码算法攻击的 新一代密码算法。

所谓“后”，是因为量子计算机的出现，现有的绝大多数公钥密码算法（、、椭圆曲线等）能被足够大和稳定的量子计算机攻破，所以可以抵抗这种攻击的密码算法可以在量子计算和其之后时代存活下来，所以被称为“后”量子密码。英文表述是：”Post-quantum Cryptography (PQC)”，或者 “Quantum-resistant cryptography”。

后量子密码，作为未来 5-10 年逐渐代替、、椭圆曲线等现行公钥密码算法的密码技术，正被越来越多的人所了解。目前，美国国家标准技术研究所 () 正在制定的新一代密码技术标准，正是后量子密码标准。

0x02 为什么需要后量子密码

时至2022年，计算机与互联网领域广泛使用的公钥加密算法均基于三个计算难题：整数分解问题、离散对数问题或椭圆曲线离散对数问题，如DH、ECDH、RSA、ECDSA。然而，这些难题均可使用量子计算机并应用秀尔算法破解。虽然人类目前还不具备建造如此大型量子计算机的科学技术（5量子比特的量子计算机造价在千万美元左右），但其安全隐患已经引起了学术研究者和政府机构的担忧。

设想有两个敌对国家，其中一国秘密发展了量子计算机，而另一国还在使用普通电子计算机的密码体系。如果前者利用量子计算机对后者的密码体系发动攻击，那么后者的信息安全体系将会瞬间崩溃。

许多密码学家都在未雨绸缪，研发全新的公钥加密算法以应对将来的威胁。1994 年，当代著名数学家和计算机科学家彼得·肖尔首次提出了大整数分解的多项式时间量子算法，并应用于密码学。他的工作表明，在量子计算时代，基于大整数分解和离散对数问题的公钥密码体系将被攻破。自第一届后量子密码学大会于2006年开办以来，本领域的研究工作愈发活跃，已成为学术和业界的关注焦点。

2015 年 8 月，美国国家安全局（NSA）宣布美国政府决定制定下一代抗量子密码标准，且“刻不容缓”。2016 年，美国国家标准与技术研究院（NIST）向全世界征集抵抗量子计算机攻击的后量子密码标准。历经 4 轮遴选淘汰， 2022 年 7 月 5 日 NIST 公布了 4 项后量子密码标准。其中 3 项基于格理论、1 项基于编码理论。

密码算法	量子计算的影响
对称密码算法(SM4,AES)	密钥加倍（Grover）
散列函数(SM3,SHA-3)	输出长度增加（Grover）
经典公钥算法(RSA,DSA,ECC)	多项式算法（Shor）
格密码	未找到有效算法
多变量密码（数字签名）	未找到有效算法
基于Hash的密码（数字签名）	未找到有效算法
基于编码的密码（加密）	未找到有效算法
超奇异同源	未找到有效算法

0x03 后量子密码算法实现途径

ⅰ. 格 (Lattice-based) 最通用的一类，几乎所有经典密码概念都可以在格密码中实现，由于其计算速度快、通信开销较小，且能被用于构造各类密码学算法和应用，因此被认为是最有希望的后量子密码技术。是在算法构造本身或其安全性证明中应用到格的密码学。格，又称点阵，是群论中的数学对象，可以直观地理解为空间中的点以固定间隔组成的排列，它具有周期性的结构。更准确地说，是在 n 维空间中加法群的离散子群，这一数学对象有许多应用，其中存在几个称为“格问题”的难题，如最短向量问题和最近向量问题。许多基于格的密码系统利用到了这些难题。

ⅱ. 编码(Code-based) 主要用于构造加密算法。代表算法：McEliece。首次发表于1978年（仅比RSA晚一年），使用的是二元戈帕码，经历了三十多年的考验，至今仍未能破解。但缺点是公钥体积极大，一直没有被主流密码学界所采纳。但随着后量子密码学提上日程，McEliece算法又重新成为了候选者。许多研究者尝试将二元戈帕码更换为其他纠错码，如里德-所罗门码、LDPC等，试图降低密钥体积，但全部遭到破解，而原始的二元戈帕码仍然安全。

ⅲ. 多变量(Multivariate-based) 构造签名方案、加密、密钥交换较有优势。是应用了有限域上多元多项式的密码学，包括对称加密和非对称加密。

ⅳ. 哈希(Hash-based) 主要用于构造数字签名。代表算法：Merkle 哈希树签名、XMSS、Lamport 签名等。

这些算法的安全性，依赖于有没有可以快速求解其底层数学问题或直接对算法本身的高效攻击算法 。这也正是量子计算机对于公钥密码算法有很大威胁的原因。

0x04 后量子密码应用现状

后量子密码可以被应用于更高层次一些的协议/应用，包括：HTTPS (TLS)、SSH、VPN、IPsec、比特币等数字货币、U 盾、桌面/移动操作系统等各个领域中。

最著名的是 2016 年 Google 在 Chrome Canary 分支版本中加入了基于 RLWE 问题的后量子密钥交换算法 NewHope 。

加密算法：

CRYSTALS-KYBER：基于格密码（Structured-lattices）

签名算法：

CRYSTALS-DILITHIUM：基于格密码
FALCON：基于格密码（Structured-lattices）
SPHINCS+：基于哈希函数（Structured-lattices）

微软研究院：

推出后量子 VPN
将其主推的后量子密码算法 Picnic 使用到 PKI(Public Key Infrastructure，公开密钥基础设施) 和 HSM(Hardware Security Module，硬件安全模块) 集群中。

二.格密码学

格密码是一类备受关注的抗量子计算攻击的公钥密码体制. 格密码理论的研究涉及的密码数学问题很多, 学科交叉特色明显, 研究方法趋于多元化。

格密码的发展大体分为两条主线: 一是从具有悠久历史的格经典数学问题的研究发展到近 30 多年来高维格困难问题的求解算法及其计算复杂性理论研究; 二是从使用格困难问题的求解算法分析非格公钥密码体制的安全性发展到基于格困难问题的密码体制的设计。

0x11 格密码简史

时间	标志事件
18世纪–1982年	格经典数学问题的讨论，代表人物：Lagrange，Gues，Hermite，MInkowski等
1982年–1996年	LLL算法的提出（Lenstra-Lenstra-Lovasz）
1996年–2005年	第一代格密码诞生（Ajtai96, AD97G, GH9）
2005年–2016年	第二代格密码出现并逐步完善，并实用化格密码算法（Regev05, GPV08,MP12 BLISS ,NewHope, Frodo）
2016年–	格密码逐步得以标准化

0x12 格密码优势

格密码	经典密码
量子攻击算法	Shor算法
矩阵乘法、多项式乘法	Shor算法
Worst-case hardness	Average-case hardnes
结构灵活、功能丰富	结构简单、功能受限

0x13 格密码发展

post		current
格经典数学问题		高维格困难问题的求解算法及其计算复杂性理论研究
使用格困难问题的求解算法分析非格公钥密码体制的安全性		基于格困难问题的密码体制的设计

0x14 格基本概念(Lattice)

1. 线性无关

，其中任何一个向量都不是它前面向量的组合，即：

存在一组数使得且。当这组数不全为0时，线性相关。

线性无关的性质：

性质1：若两个向量组 ,(1)中任意向量可由(2)线性表示，(2)中任意向量可由(1)线性表示，那么这两个向量组等价。

性质2：向量组线性无关，线性相关，则可由线性表示且表示式唯一。

2. 定义

设是一组线性无关的向量。由生成的格是指向量的线性组合构成的向量集合，且其所使用的系数均在中，即：

$L = \{a_1v_1+a_2v_2+\dots+a_nv_n:a_1,a_2,\dots,a_n \in Z \}$

严格地说，格是m维欧式空间的个线性无关向量组的所有整系数线性组合。

3. 基与维度

任意一组可以生成格的线性无关的向量都称为格的基，格的基中的向量个数称为格的维度。某种程度上，格可以理解成系数为整数的向量空间。简单来说，对于二维坐标系，向量和就是最简单的一组格基。一般来说，达到足够安全性的方案，格的维度在 1000 左右。

4. Hadamard比率

用来描述 n 维线性空间某一组基的正交程度，其中是行列式，是L2范数，是绝对值。越接近 1，基B的正交性越好，若等于 1，那么B是正交基。

$H(B):=\frac{|det(B)|}{\prod \limits_{i=1}^n||b_i||} \quad ,\quad 0<H(B)\leq 1$

5. Gram_Schmidt正交化 (施密特正交化)

正交：非0向量内积为0，即

$[x,y] = x^{T}y = 0$

标准正交基：向量是标准正交的，当且仅当

$q_i^{T}q_j = \left\{ \begin{aligned} 0,if \quad i \neq j (正交向量)\\ 1,if \quad i = j(单位向量) \end{aligned} \right.$

Schmit正交化：给定 n 个线性无关向量，被定义为

$\widetilde b_i:=b_i-\sum_{j=1}^{i-1}\mu_{ij}\widetilde b_{j}, \,where \quad \mu_{i,j} = \frac{<b_i,\widetilde b_j>}{<\widetilde b_j,\widetilde b_j>}$

此处写一下三维的施密特正交公式：

$\beta_1 = \alpha_1 \\ \beta_2 = \alpha_2 - \frac{(\beta_1,\alpha_2)}{(\beta_1,\beta_1)} \beta_1 \\ \beta_3 = \alpha_3 - \frac{(\beta_1,\alpha_3)}{(\beta_1,\beta_1)}\beta_1 - \frac{(\beta_2,\alpha_3)}{(\beta_2,\beta_2)}\beta_2$

6. 约减基

约减的主要目的是将这组任意给定的基转化为一组正交性较好的优质基，并使得这个优质基中的各个向量尽量短。

如果以下情况成立，基是一个约减基:

$1. \begin{flalign} \quad\forall 1 \leq i \leq n, j < i ,|\mu_{i,j}| \leq \frac{1}{2} \end{flalign} \\ 2.\quad\forall 1\leq i < n , \delta ||\widetilde b_i||^2 \leq ||\mu_{i+1,i} \widetilde b_i + \widetilde b_{i+1} ||^2$

根据施密特正交，可以看出与两个基向量的夹角有关。

7.素数有限域 $𝕢$

即我们的世界里面只存在这个范围内所有整数。

8.无限范数(Infinity Norm)

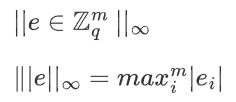
即：找这个维度为 m 的向量 e 中的每一个值，然后返回最大值。

9.最大值封顶的随机分布

从这个随机分布中取出的每一个随机值都小于 B 。

$\forall x \gets x_{B}^{m}:|| x ||_{\infty} \leq B$

0x15 格的困难数学问题

密码学方案的安全性的一个重要条件是：底层的数学问题是困难的。对于格密码，自然就是格中的困难问题需要是真正困难的，所以研究格问题的困难性是很重要的研究方向。

✍最短向量问题(Shortest Vector Problem,SVP)

对于给定的格，找到非零的格向量，使得对于任意非零向量

✍近似最短向量问题(Approximate Shortest Vector Problem,aSVP)

对于给定的格，找到非零的格向量，使得对于任意非零向量

✍唯一最短向量问题(Unique Shortest Vector Problem,uSVP)

对于给定的格，满足 $\lambda{2}(L) \gt \gamma \lambda{1}(L)$，找到格的最短向量

✍近似最短向量判断问题(GapSVP)

对于给定的格 L 和有理数 r，如果有 $\lambda{1}(L) \leq r$，则返回是；如果 $\lambda{1}(L) \leq \gamma r$，则返回否。其它情况随机返回是或否。

✍小整数问题(SIS)

给定模数，常实数和矩阵，其中。如何寻找一个非零向量，使得且。

✍搜索型误差学习(LWE)

给定一个维数，模数，$Zq $上一概率分布为。随机从分布$ Z{q}^{n} \times Z{q} $中均匀抽样或者$ A{s,X} $中独立抽样，如果判断此抽样来自$ A{s,X} $则返回，如果来自$ Z{q}^{n} \times Z_{q}$ 返回 “NO”。

0x16 高斯格基约减算法(Gauss Lattice Reduction)

此算法是二维情况，思想和 LLL 有相似之处，都是不断实施先约化后交换的策略。

对于两个向量，满足；如果，则交换和。$v_2^* = v_2 - mv_1,m = [\frac{}{||v_1||^2}]$。这个想法基于Schmit正交化，为了满足格的整系数条件做了系数四舍五入的处理。

算法步骤：

m=0 时约化结束，下面证明最后返回的是格中最短向量，此时满足 $|\frac{}{||v_1||^2}| \leq 0.5 $。

设

$\begin{align*} ||v||^2 &= a^2||v_1||^2 + b^2||v_2||^2 + 2ab<v_1,v_2> \\ &\ge a^2|| v_1 ||^2 + b^2||v_2||^2 - 2ab<v_1,v_2> \\ &\ge a^2|| v_1||^2 - ab||v_1||^2 + b^2||v_1||^2 \\ &= (a^2-ab+b^2)||v_1||^2 \\ &a^2 - ab + b^2 = (a-\frac{1}{2}b)^2 + \frac{3}{4}b^2 \end{align*}$

上式必为非负整数，当且仅当时等式左右相等，故

$||v|| \geq ||v_1||$

算法递归实现：

def Gauss_Reduction(v1,v2):
    if v1.norm() > v2.norm():
        v1,v2 = v2,v1
    m = round((v1*v2)/v1.norm()^2)
    if m == 0 : return (v1,v2)
    else : 
        v2 = v2 - m*v1 
        return Gauss_Reduction(v2,v1)

算法循环实现：

def Gauss_Algorithm(x,y):
    v1 = x; v2 = y
    finish = False

    while not finish:
        m = round(v2.dot_product(v1)/v1.dot_product(v1))
        v2 = v2 - m*v1
        if(v1.norm() <= v2.norm()):
            finish = True
        else: v1,v2 = v2,v1
    return v1,v2

0x17 LLL算法

LLL算法是最短向量问题(SVP)的近似算法，是1982年由K.Lenstra, H.W.Lenstra, Jr. and L.Lovasz 设计的，后被称为LLL算法，给出了一个的近似比例 (approximation ratio)，其中是格的维数。

LLL 算法可以看作是高斯约减算法在高维情况下的推广，本质是：把给定的向量基转化为一组正交性较好的优质基，并使得这个优质基中的各个向量尽可能短。

首先用矩阵形式描述 Schmit正交化 过程。

$(v_1\,v_2\,\dots\,v_n)=(v_1^*\,v_2^*\,\dots v_n^*)* \begin{bmatrix} 1 & u_{1,2} & u_{1,3} & \dots & u_{1,n} \\ & 1 &u_{2,3} & \dots & u_{2,n} \\ & & & \dots & \\ & & & & 1 \end{bmatrix} \\ u_{i,j} = \frac{<v_i^*,v_j>}{||v_i^*||^2}$

令${v1,v_2,\dots,v{n}} $为格$ L $的一组基，$ LLL $算法可以在有限步骤内终止，并且能返回的一组$ LLL$约减基，检测到满足条件后直接输出。

1.sizereduce：任意 $i<j \leq n , |u{i,j}| \leq 0.5$

2.Lovász condition：$||vi^*||^2 \geq (\frac{3}{4}-u{i-1,i}^2)||v_{i-1}||^2$

注：对于 Lovász condition 可以有多种表达式，另一种常见且正确的表达式为

$||v_i^* + \mu_{i,i-1}v_{i-1}^*||^2 \ge \frac{3}{4}||v_{i-1}^*||^2$

def max(a, b):
    return a if a > b else b

def LLL_v0(M, delta=0.75):
    B = deepcopy(M)
    Q, mu = B.gram_schmidt()
    n, k = B.nrows(), 1
    
    while k < n:
        
        # size reduction step
        for j in reversed(range(k)):
            if abs( mu[k][j] ) > 0.5:
                B[k] = B[k] - round( mu[k][j] ) * B[j]
                Q, mu = B.gram_schmidt()
        
        # swap step 
        if Q[k].dot_product(Q[k]) >= (delta - mu[k][k-1]^2) * Q[k-1].dot_product(Q[k-1]):
            k = k + 1
        else:
            B[k], B[k-1] = B[k-1], B[k]
            Q, mu = B.gram_schmidt()
            k = max(k-1,1)
    
    return B

经过LLL格约减算法后得到的一组基有着一些良好的性质，这组基可以在多项式时间内得到，利用这些性质我们可以很容易地求解某些问题，例如，通过使用LLL格约减算法可以在一个令密钥持有者十分不安的时间内，破解那些使用基于背包密码体制问题的密码系统密钥。

LLL算法复杂度：

$log_{\frac{1}{\sqrt\delta}}D_{B} \leq \frac{1}{log\, 1 / \sqrt(\delta)} · \frac{n(n-1)}{2}·log(max||b_i||)$

LLL算法与欧几里得算法的联系：

LLL often gets compared to Euclid’s Algorithm for finding GCDs. This is an imperfect analogy, but at a high-level they have a core similarity. Namely, both LLL and Euclid’s algorithm could be broken down into two steps: “reduction” and “swap”.

def euclid_gcd(a, b):
    if b == 0: # base case
        return a 
    x = a mod b # reduction step 
    return euclid_gcd(b, x) # swap step

# dont try to grok this yet...
def lll(basis):
    while k <= n:
        for j in reverse(range(k-1, 0)): # reduction step loop
            m = mu(k,j)
            basis[k] = basis[k] - mu*basis[j] # vector reduction
            # update orthogonalized basis 
    if lovasz_condition:
        k += 1
    else:
        basis[k], basis[k+1] = basis[k+1], basis[k] # swap step
        # update orthogonalized basis
        k = max(k-1,1)
    return basis

0x18 LWE(Learning With Errors)

1.有噪声的高斯消除问题(Gaussian Elimination with Noise)

线性代数我们学了，高斯消除法是在行与行之间操作求解未知数的方法，即：给定一个矩阵和一个向量，能否找到一个向量，使得关系满足。

增加噪声后，问题变为：

给定一个矩阵和一个向量，其中是我们在一个固定数值范围内随机采集的一个随机噪音向量(扰动变量，服从某种公开的分布)，那么我们能否通过和的值来还原(Learn)最初的未知数向量？

我们把这一类的问题称为 误差还原问题(LWE)。

2005 年, Regev 提出了带错误的学习问题 (LWE), 证明了 LWE 与格上困难问题 (如近似最短向量问题 Gap-SVP) 相关, 并给出了基于 LWE 的公钥密码方案. 与之前出现的格上困难问题比较, LWE 在构建密码系统时更方便。

2.搜索LWE问题(Search LWE)

定义如下：

$LWE(n,m,q,x_{B}):Search \quad Version \\ Let \, A \gets \mathbb{Z}_{q}^{m\times n},s \stackrel{R} \gets \mathbb{Z}_q ,e \stackrel{R} \gets x_{B}\\ Given(A,As+e),find \,s'\in \mathbb{Z}_{q}^{n}\,s.t. ||As'-(As+e)||_{\infty} \leq B \\$

m：这个线性方程组有多少组方程，一般来说都是n的一个多项式倍数即。m越大，问题越简单。

n：每个方程中有多少个未知数，是LWE问题的安全参数(Security Parameter)，n越大，问题越难。

q：有限域的大小，一般会选足够大的素数，一般也是 n 的多项式倍数，可以设置为。

B：误差上限，要满足。可理解为：LWE问题中 需要找到的解v 距离 实际取值 究竟差多少。

所以LWE问题的本质就是：给定矩阵以及有误差的乘积，还原出未知的向量 。

困难性来源于方程的误差。

LWE的直观困难性有很多：

求解方法	计算复杂度
穷举搜索
搜索s
q-ary格

3.决策LWE问题(Decisonal LWE)

密码学中，一般需要证明一个困难问题的安全性的时候，我们一般都会使用决策版本的LWE问题（Decisional LWE）。决策LWE（简称为DLWE）的设定和搜索LWE（简称为SLWE）基本相同。

$LWE(n,m,q,x_{B}):Decisional \quad Version \\ Let \, A \gets \mathbb{Z}_{q}^{m\times n},s \stackrel{R} \gets \mathbb{Z}_q ,e \stackrel{R} \gets x_{B},v \stackrel{R} \gets Z_{q}^{m} \\ Distinguish(A,As+e)from(A,v) \\$

唯一不同的是，SLWE最后的问题是需要我们找到，而DLWE只需要让我们辨别看到的到底是LWE问题中的误差乘积 还是一个随机生成的向量。

基于格的密码分析

格理论第一次在密码学中应用, 是作为一种分析工具出现的。

很多非基于格的密码体制的安全性分析，可以归约到求解格中困难问题，进而利用求解这些困难问题的算法进行分析。这些研究从一开始就将基于经典数学难题— 分解因子问题与离散对数问题的公钥密码体制的安全性分析的研究方法进行了跨学科的思维转换，从而让人们意识到格理论的研究对公钥密码分析的重要性。

Shamir 在 1982 年第一次提出破解基本的 Merkel-Hellman 背包密码体制的多项式时间算法。其主要思想是利用 H. W. Lenstra 等人的理论，即利用多项式时间内求解关于固定数量变元的整数规划 解决背包密码算法中的问题。该方法是 LLL 算法的雏形。随后, Lagarias将背包问题归约为找格中的短向量问题，通过更有效的 LLL 算法求解。 1985 年，Lagarias 和 Odlyzko 构造了一类格，利用 LLL 算法求解格的短向量，从而破解了密度小于 0. 6463 的背包体制。后来通过构造不同的背包格,，该结果被改进到 0.9408。

过去 30 年来该领域丰富的研究成果表明了该领域受关注的程度。它的学科交叉所带来的许多数学问题不仅成为密码领域重点研究的内容，也被数学领域与计算机科学领域所关注。格密码体制由于其运算具有线性特性比 RSA 等经典公钥密码体制具有更快的实现效率。又由于该类密码体制安全性基于 NP-Hard 或者 NP-C 问题，使得格密码体制成为抗量子攻击的密码体制中最核心研究领域。此外，由于格运算具有同态特性，因此设计格同态加密密码体制对于解决安全云计算环境下的密文检索，加密数据处理等方面具有潜在的应用价值。尽管如此，格密码理论还待于完善与发展，无论是理论研究还是实用化密码体制的设计都具有很大的理论价值和实际意义。