Meta Field
0%

大数据隐私保护实验三

发表于 更新于 分类于 Valine：
本文字数： 6.5k 阅读时长 ≈ 6 分钟

满昏

k-anonymity

使用 概括 和 隐匿 技术，得到精度较低的数据，使得同一个准标识符至少有 条记录，使得 攻击者 无法通过准标识符连接记录，从而无法获得 敏感数据 ( Sensetive Attributes)。

✍概括

对数据进行更 概括性、抽象的 描述，使无法区分具体值

比如在数据库表中，年龄 是 18、20、23……，经过概括技术后为一个年龄段，比如 20 岁以上。

✍隐匿

即不发布某些信息，从而降低精度

20 岁 2 ； 38 岁 3

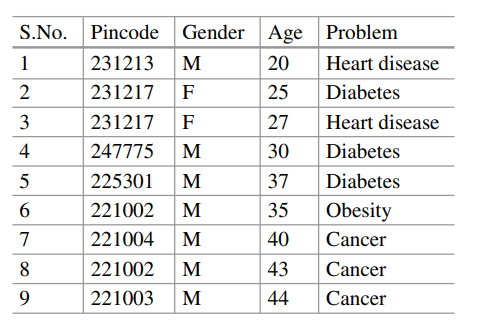
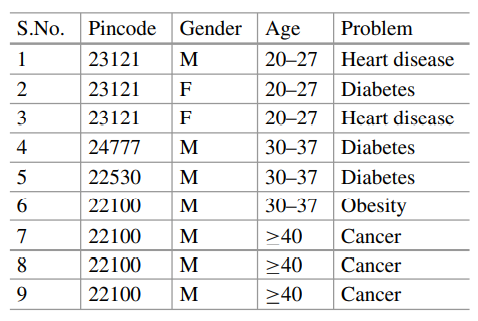
上图为原始数据表，下图为 k=2 匿名处理后的数据表

K-匿名技术 虽然可以阻止身份信息的公开，但无法防止属性信息的公开，导致其无法抵抗同质攻击，背景知识攻击等情况。

K-匿名技术在计算上也很昂贵：朴素算法是 ，更快的算法占用空间非常大。

差分隐私

汉明距离

本质：通过比较二进制每一位是否相同来计算二进制数据的相似度，若不同则汉明距离+1。

eg：

000 和 001 汉明距离为 1

000 和 111 汉明距离为 3

二进制数据相似度越 高 ，对应汉明距离越 小

直观原理

有个人叫 Alice ，她的信息在数据集 中，把 Alice 的信息换成 Bob 的信息，组成新的数据集 ,此时我们知道，这两个数据集的差别就是 Alice 的数据。

有个攻击者 Eve，他从这得到了信息 ，如果他无法判断 是来自于 还是 ，那么我们认为 Alice 的隐私受到保护。因此，差分隐私要求被发布的信息要经过 随机算法 处理，且该随机算法会对信息做一些 扰动 。

符号

查询函数，比如查询 最大值、均值 等

实数概念，无上标表示 一维数据 ； 表示 n 维数据1，比如 梯度

随机噪声，可以服从 高斯分布 或 指数分布

兄弟数据集，二者之差一个样本，即汉明距离为 1

最终结果，

一个很小的值，用来衡量隐私预算，一般来讲，值越小越好，但假如噪声就越大，数据可用性就下降了。

松弛项，表示 可以接受差分隐私在一定程度上的不满足

理论

一随机算法 满足 - 差分隐私 ，当且仅当

修改一个数据不会对算法 的输出分布带来太大影响。

但是上述差分隐私定义过于严格，实际应用需要很多隐私预算，为了保证算法实用性，引入了松弛版本的差分隐私：

实验技术要点

✍数据清洗与处理

✍生成 匿名

✍差分隐私

数据清洗

数据的质量最终决定了数据分析的准确性，数据清洗是唯一可以提高数据质量的方法,使得数据分析的结果也变得更加可靠。

本实验的数据集主要针对 缺失数据 的处理

首先把数据集每一行存到一个变量里面：

1
2
3
4
5
6
data_list = []
def read_data_list():
	with open("adult.data.txt","r") as f:
		for line in f.readlines():
			line = line.strip('\n').split(', ')
			data_list.append(line)

事实上，我们总会遇到数据缺失。对此，我们可以将存在缺失的行直接删除，但这不是一个好办法，还很容易引发问题。因此需要一个更好的解决方案。最常用的方法是，用其所在列的均值来填充缺失。为此，可以利用 scikit-learn 预处理模型中的 inputer 类来很轻松地实现。机器学习中有关 类，对象，方法 的相关概念：

👋类

类是我们要构建的模型，如果我们希望搭建一个棚子，那么搭建规划就是一个类。

👋对象

对象是类的一个实例。在这个例子中，根据规划所搭建出来的一个棚子就是一个对象。

👋方法

传递给它某些输入，它返回一个输出。这就像，当我们的棚子变得有点不通气的时候，可以使用「打开窗户」这个方法。

也许在某些项目中，你会发现，使用缺失值所在列的 中位数 或 众数 来填充缺失值会更加合理。填充策略之类的决策看似细微，但其实意义重大。因为流行通用的方法并不一定就是正确的选择，对于模型而言，均值也不一定是最优的缺失填充选择。

本实验中，如果发现数据集中某一行有 ，那就去掉对应行

1
2
3
4
5
6
7
8
9
10
def remove_invalid(data_list):
	res = []
	for data in data_list:
		flag = 1
		for attr in data :
			if attr == '?':
				flag = 0
			if flag:
				res.append(data)
		return res

生成k匿名

1
2
3
这段代码实现了一个检查k-匿名数据集的函数check_k_anonymity，其输入参数为data_list，即待检查的数据集。函数的返回值是一个字典类型的变量k_dict，其中字典的key是数据集中的标识符，value是标识符出现的次数，即k值。

该函数首先创建一个空的字典k_dict，然后遍历数据集data_list中的每条数据。对于每条数据，它会提取出标识符（假设标识符是数据的最后一个元素），并检查字典k_dict中是否已经存在该标识符。如果不存在，则将该标识符添加到字典中，并将其值设置为1；如果已经存在，则将该标识符的值加1。最后，函数返回字典k_dict，其中每个key-value对代表一个标识符及其出现次数。
1
2
3
4
5
6
7
8
9
def check_k_anonymity(data_list):
    k_dict = {}
    for data in data_list:
        strid = data[-1]
        if strid not in k_dict:
            k_dict[strid] = 1
        else:
            k_dict[strid] += 1
    return k_dict
1
2
3
4
5
6
7
8
9
10
11
该代码实现了一个数据泛化算法，旨在从给定的输入数据集data_list中实现k-匿名化的数据集。

generalize函数接受两个参数：data_list（输入数据集）和k（应该具有相同属性值的记录数的最小值，即k-匿名级别）。

代码首先定义了两个列表：nodigit_index和digit_index。前者包含数据集中非数字属性的索引，后者包含数字属性的索引。然后，该函数使用itertools.combinations方法生成所有可能的数字属性组合。

接下来，函数遍历每个数字属性组合，并对data_list中的每个数据记录，用星号替换选定属性的前两个字符，从而使其泛化。如果数据记录的长度小于或等于15，则添加新标识符；否则，用新标识符替换现有标识符。

然后，函数使用check_k_anonymity函数计算泛化后数据集的k-匿名级别。如果k-匿名级别小于指定的最小级别k，则函数会删除任何不满足k-匿名标准的记录。然后，它计算泛化后数据集的新k-匿名级别，并跟踪产生最接近k的最高k-匿名级别的最佳数字属性组合。

最后，函数打印最佳数字属性组合和达到的k-匿名级别。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
def generalize(data_list,k):
    initial_len = len(data_list)
    nodigit_index = [1,3,5,6,7,8,9,13]
    
    digit_index = [0,2,4,10,11,12]
    # 获取不同属性的组合
    combinations = list(itertools.combinations([0,1,2,3,4,5,6],2))


    distance = 40000
    best_method = ['02',1]
    for c in combinations:
        for data in data_list:
            _id = ""
            for i in digit_index[c[0]:c[1]]:
                # 对每一条数据的属性值前两个字符保留后替换为 * 
                data[i] = data[i][:1] + "*"
                _id += data[i]
            if len(data) <= 15:
                data.append(_id)
            else:
                data[15] = _id

        k_dict = check_k_anonymity(data_list)

        k1 = min(k_dict.values())
        print("准标识符选取为{},匿名处理后 k = {}".format(attrs[c[0]:c[1]],k1))
        if(min(k_dict.values()) < k):
            print("未满足要求，正在筛选中...")

        res = []
        for data in data_list:
            if k_dict[data[15]] < k:
                data[15] = "000"
                # 未达到要求
    
        for data in data_list:
            if data[15] != "000":
                res.append(data)

        print("去除了"+str(initial_len-len(res))+"条数据")
    
        final_k = min(check_k_anonymity(res).values())
        print("去除后 k = " + str(final_k))

        if distance > final_k - k:
            distance = min(final_k - k,distance)
            best_method = [attrs[c[0]:c[1]],final_k]

        if final_k == k:
            print(str(k)+"匿名处理成功")
            print('-----------------------------------------------------------')
            break
        else:
            print(str(k)+"匿名处理失败，本方案能够完成的最接近的为"+str(final_k)+"匿名处理")
            print('-----------------------------------------------------------')
    print('总结得最佳方案是选取：{}作为准标识符，能够完成{}匿名处理'.format(best_method[0],best_method[1]))
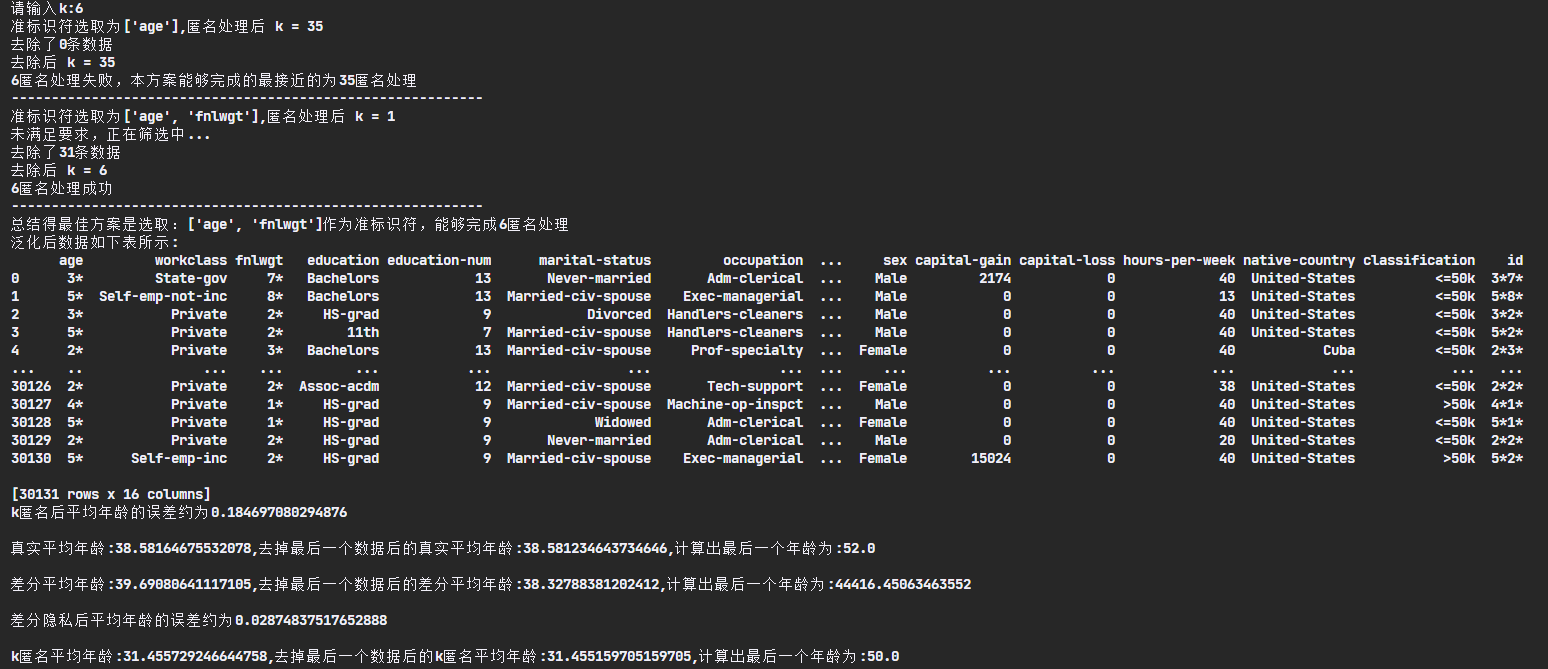
1
2
3
4
5
6
7
8
9
def show_data_list(data_list):
    res = []
    for data in data_list:
        if data[15] != "000":
            res.append(data)
    df = pd.DataFrame(res,
                columns=['age','workclass','fnlwgt','education','education-num','marital-status','occupation','relationship','race','sex','capital-gain','capital-loss','hours-per-week','native-country','classification','id'])
    print('泛化后数据如下表所示:')
    print(df)

差分隐私

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
if __name__ == "__main__":
    #读入数据
    read_data_list()
    #去除含有问号的数据行
    data_list = remove_invaild(data_list)
    #获取用户输入要求的k
    target_k = int(input("请输入k:"))
    #泛化处理
    generalize(data_list,target_k)
    show_data_list(data_list)

    #计算初始数据集年龄均值
    real_ages = []
    with open("adult.data.txt", "r") as f:
        for line in f.readlines():
            line = line.strip('\n').split(', ')  #去掉读取每一行的换行符并分割为列表
            real_ages.append(int(line[0]))

    length = len(real_ages)
    real_avg = sum(real_ages)/length

    cf_avg = real_avg + np.random.laplace(loc=0, scale=1)

    k_ages = []
    for data in data_list:
        k_ages.append(int(data[0][:1]) * 10)
    k_avg = sum(k_ages)/length

    print('k匿名后平均年龄的误差约为{}\n'.format(abs(real_avg - k_avg) / real_avg))
    
    real_ages.pop()
    real_avg2 = sum(real_ages) / (length-1)
    print("真实平均年龄:{},去掉最后一个数据后的真实平均年龄:{},计算出最后一个年龄为:{}\n".format(real_avg,real_avg2, real_avg*length - real_avg2*(length-1)))
    
    cf_avg2 = real_avg2 + np.random.laplace(loc=0, scale=1)
    print("差分平均年龄:{},去掉最后一个数据后的差分平均年龄:{},计算出最后一个年龄为:{}\n".format(cf_avg,cf_avg2,cf_avg*length-cf_avg2*(length-1)))
    
    print('差分隐私后平均年龄的误差约为{}\n'.format(abs(real_avg - cf_avg) / real_avg))
    k_ages.pop()
    k_avg2 = sum(k_ages) / (length-1)
    print("k匿名平均年龄:{},去掉最后一个数据后的k匿名平均年龄:{},计算出最后一个年龄为:{}\n".format(k_avg,k_avg2, k_avg*length - k_avg2*(length-1)))

-------------本文结束感谢您的阅读-------------
请作者喝一杯蜜雪冰城吧！