Meta Field
0%

大数据隐私保护实验二

发表于 更新于 分类于 Valine：
本文字数： 11k 阅读时长 ≈ 10 分钟

满昏

Lab-02

技术要点

👋读取数据集

👋保序加密

👋树

👋数据查询

读取数据集

1
2
3
4
5
6
data_list = []
def read_data_set():
    with open("NE.txt","r") as f:
        for line in f.readlines():
            line = line.strip('\n').split(' ')
            data_list.append(line)

readline : 逐行读取文件内容，将每一行字符串存储到 line 变量中，然后使用 strip('\n') 方法去除每行字符串末尾的换行符，并使用 split(' ') 方法将每行字符串按空格分割成一个列表 line。

保序加密(Order Preserving Encryption)

OPE 是一种密文保持明文顺序的特殊加密方案，它既能保护用户数据机密性，也能实现密文数据高效查询。

当进行范围查询时, 用户只需要提供查询区间两个端点的加密密文给服务器。随后, 云服务器根据用户提供区间端点的加密密文与 原有数据库的密文 进行比较。最后, 服务器返回给用户符合查询要求的密文数据, 用户解密即可。

保序加密方案的形式化定义如下：

一个保序加密方案可以描述为一个四元组

​ · : 根据安全参数，生成秘密状态 ；

​ · : 在状态 下, 加密明文 为密文 , 并将状态 更新为状态 ;

​ · : 在状态 下, 输入查询区间 , 输出查询结果的密文数据集 ;

​ · : 在状态 下, 解密密文 为明文 .

如果加密方案满足: 对任意的 有 , 则称这个方案为保序加密方案。

本实验采用 基于线性隐藏和增加噪音 的保序加密方案，下面这一串叫 索引 。

其中 需要保密， 是满足索引保序的随机数，而且 的输入不能破坏索引 的输入顺序。

KD树

KD树概念与结构

简称k维树，是一种空间划分的数据结构，每一个节点都是k维的数据。

KD树可以看做是二分查找树 (BST) 的高维存在，BST可以被认为是KD树在一维数据上的特例。KD树常被用于高维空间中的搜索与查询，比如范围搜索和最近邻搜索。KD树是二进制空间划分树的一种特殊情况。在激光雷达SLAM中，一般使用的是三维点云。所以，KD树的维度是3。

数据结构如下：

1
2
3
4
5
6
7
8
struct kdtree{
    Node-data - 数据矢量   数据集中某个数据点，是n维矢量（这里也就是k维）
    Range     - 空间矢量   该节点所代表的空间范围
    split     - 整数       垂直于分割超平面的方向轴序号
    Left      - kd树       由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
    Right     - kd树       由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
    parent    - kd树       父节点  
};

一般情况下，会用到的数据是{数据矢量，切割轴号，左支节点，右支节点}。这些数据就已经满足 KD树的 构建 和 检索。

KD树 一般会在两个方面使用：

  • 最近邻搜索
  • 距离范围搜索

KD树构建

构建KD树是针对高维数据，需要针对每一维都进行二分。

  1. 建立根节点；

  2. 选取方差最大的特征作为分割特征；

  3. 选择该特征的中位数作为分割点；

  4. 将数据集中该特征小于中位数的传递给根节点的左儿子，大于中位数的传递给根节点的右儿子；

  5. 递归执行步骤2-4，直到所有数据都被建立到KD Tree的节点上为止。

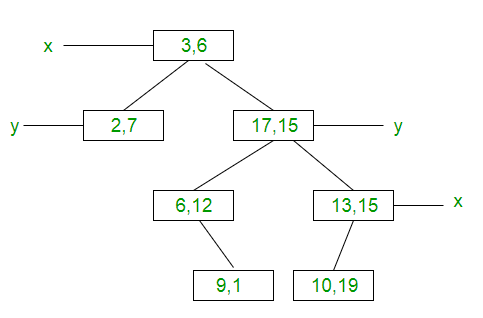
以上述 2维KD树 为例讲解：

第一层以 x 坐标为比较依据(only x)，比 x 小的放在左孩子，其余放在右孩子(包含相等情况)；

第二层以 y 坐标为比较依据(only y)，比 y 小的放在左孩子，其余放在右孩子(包含相等情况)；

然后一直往下进行直到所有结点都放好。

1
2
3
4
5
6
7
8
9
10
11
12
def insertNode(root, point, depth):
	if not root:
		return newNode(point)
	cd = depth % K
	if point[cd] < root.point[cd]:
		root.left = insertNode(root.left, point, depth + 1)
	else:
		root.right = insertNode(root.right, point, depth + 1)
	return root

def insert(root, point):
    insertNode(root,point,0)

KD树查找

查找 和 植树的内容 大同小异。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def areSame(point1, point2):
	for i in range(K):
		if point1[i] != point2[i] :
			return False
	return True

def searchNode(root, point, depth):
	if not root:
		return False
	if areSame(root.point, point):
		return True
	cd = depth % K
	if point[cd] < root.point[cd] :
		return searchNode(root.left, point, depth)		
	return searchNode(root.right, point, depth)

def search(root, point):
    return searchNode(root, point, 0)

KD树代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
# 2维 KD树
import sys
K = 2

class Node:
    def __init__(self,point):
        self.point = point 
        self.left = None
        self.right = None

def newNode(point):
    return Node(point)

def insertNode(root, point, depth):
	if not root:
		return newNode(point)
	cd = depth % K
	if point[cd] < root.point[cd]:
		root.left = insertNode(root.left, point, depth + 1)
	else:
		root.right = insertNode(root.right, point, depth + 1)

	return root

def insert(root,point):
    return insertNode(root,point,0)

def areSame(point1,point2):
    for i in range (K) :
        if point1[i] != point2[i]:
            return False 
        
    return True 

def searchNode(root,point,depth):
    if not root:
        return False
    if areSame(root.point,point):
        return True

    cd = depth % K
    if point[cd] < root.point[cd] :
        return searchNode(root.left,point,depth+1)
    return searchNode(root.right,point,depth+1)

def search(root,point):
    return searchNode(root,point,0)

def judgeFoundNode(root,point):
    if search(root,point):
        print("Found")
    else:
        print("Not Found")

if __name__ == '__main__' :
    root = None
    points = [[3, 6], [17, 15], 
            [13, 15], [6, 12], 
            [9, 1], [2, 7], [10, 19]]
    n = len(points)
    # 种树
    for i in range(n):
        root = insert(root,points[i])

    point1 = [10,19]
    point2 = [12,19]
    judgeFoundNode(root,point1)
    judgeFoundNode(root,point2)

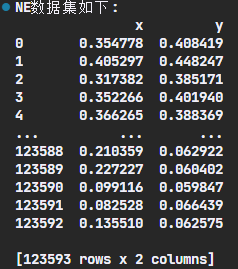
实验过程

step1 读取文件并显示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import pandas as pd

data_list= []
def read_data_set():
    with open("NE.txt","r") as f :
        for line in f.readlines():
            line = line.strip('\n').split(' ')
            data_list.append(line)
        
if __name__ == '__main__':
    read_data_set()
    print("NE数据集如下:")
    print(pd.DataFrame(data_list,
                        columns=['x','y']))

实验结果截图

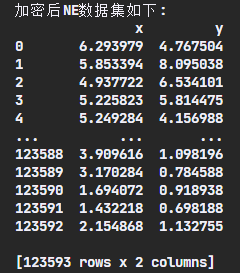
step2 数据集加密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def encrypt_data(message):
    a = random.uniform(10.0,20.0)
    b = random.uniform(1.1/100000,2.1/100000)
    noise = random.uniform(0,0.000005)
    encrypted = a*message + b + noise
    return encrypted

encrypted_list = []
    for data in data_list :
        data[0] = encrypt_data(float(data[0]))
        data[1] = encrypt_data(float(data[1]))
        data = tuple(data)
        encrypted_list.append(data)

    print("加密后NE数据集如下:")
    print(pd.DataFrame(encrypted_list,
                        columns=['x','y']))

✍python 元组 tuple

tuple 与 list 类似，不同之处在于 tuple 的元素不能修改。

元组使用 小括号，列表使用 方括号。

✍遇到的问题：

1
TypeError: can't multiply sequence by non-int of type 'float'

原因分析：两个数据类型不一致，不能相乘。

在我的代码中：

用 float 强制转换是因为 data 是列表类型，而加密函数中乘 a 是 float 类型，因此会报错，所以要强制转换。

数据集加密测试结果截图：

step3 植树

对于 树 这个我们熟悉而陌生的数据结构，首先要构造结点，结点是 树 的结合。

所以先构造初始化结点 Node

1
2
3
4
5
class Node:
    def __init__(self,point):
        self.point = tuple(point) 
        self.left = None
        self.right = None

下一步：开始叠树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class KD_tree:
    def __init__(self, k) -> None :
        self.k = k
    def create_KD_tree(self, new_data, depth):
        if not new_data:
            return None
        mid_index = len(new_data) // 2  # 中位数坐标
        cd = depth % self.k 
        # 针对维度 cd 进行分类，是从 chatgpt 学会的
        sorted_new_data = sorted(new_data,key=(lamda p:p[cd]))
        median = new_data[mid_index]
        cur_Node = Node(median)
        left_children = sorted_new_data[:mid_index]
        right_children = sorted_new_data[mid_index+1:]
    	cur_Node.left = create_KD_tree(left_children, depth+1)
        cur_Node.right = create_KD_tree(right_children, depth+1)
        return cur_Node
    
   	def search(self, tree, new_data):
        self.near_point = None
        self.near_val = None
        
        def distance(self, point1, point2):
            res = 0
            for i in range(self.k):
                res += (point1[i]-point2[i])**2
            return res ** 0.5
        
        def dfs(node, depth):
            if not node:
                return 
            cd = depth % self.k
            if new_data[cd] < node.point[cd]:
                dfs(node.left, depth + 1)
            else :
                dfs(node.right, depth + 1)
                
            dist = self.distance(new_data, node.point)
            if not self.near_val or dist < self.near_val:
                self.near_val = dist
                self.near_point = node.point
                
            if abs(new_data[cd] - node.point[cd]) <= self.near_val: 
                if new_data[cd] < node.point[cd]: 
                    dfs(node.right, depth + 1) 
                else:
                    dfs(node.left, depth + 1)
            

        dfs(tree, 0)
        return self.near_point

step4 main函数

分为两部分，一部分是完成安全检索的目标，另一部分是对结果进行验证。

part1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
read_data_set()
    print("NE数据集如下:")
    print(pd.DataFrame(data_list,columns=['x','y']))
    encrypted_list = []
    for data in data_list :
        data[0] = encrypt_data(float(data[0]))
        data[1] = encrypt_data(float(data[1]))
        # 这里用 float 是因为 data 是列表类型
        # 而加密函数中乘的 a 是 float 类型
        # 所以强制转换一下，否则报错
        data = tuple(data)
        encrypted_list.append(data)

    print("加密后NE数据集如下:")
    print(pd.DataFrame(encrypted_list,columns=['x','y']))

part2

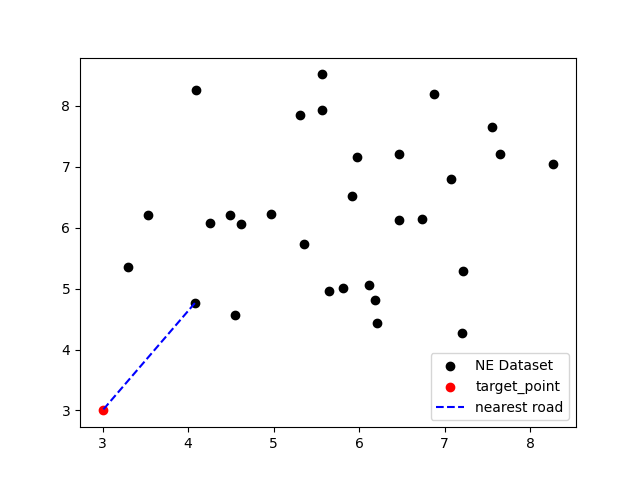
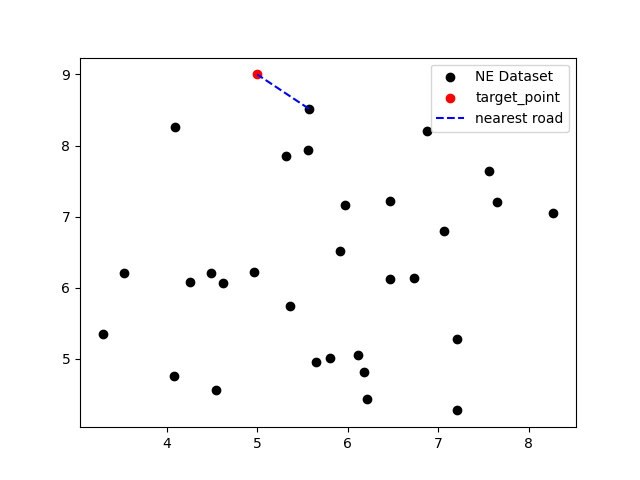
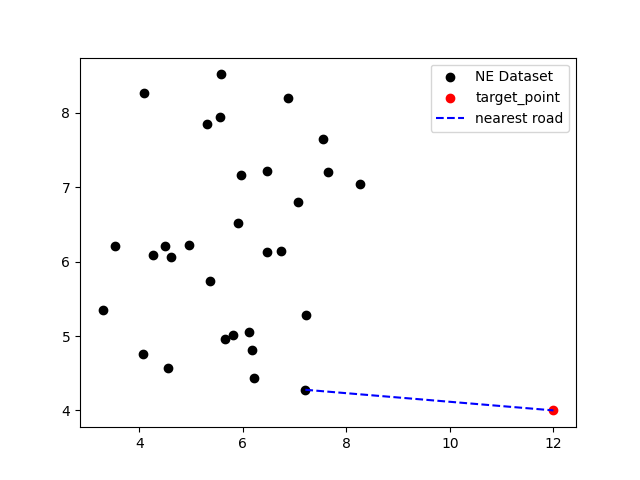
1
2
3
4
5
6
7
8
9
10
11
12
13
14
while 1:
    data_set = encrypted_list[:30]
    target_point = input("请输入查询坐标:").split(',')
    target_point = list(map(float,target_point))
    kd_tree = KD_tree(2)
    tree = kd_tree.create_KD_tree(data_set, 0)
    near = kd_tree.search(tree,target_point)
    print('离{}最近的点为: {}'.format(tuple(target_point),near))
    
    plt.scatter([x[0] for x in data_set],[x[1] for x in data_set],c = 'black', label = 'NE Dataset')
    plt.scatter(target_point[0],target_point[1],c = 'red', label = 'target_point')
    plt.plot([near[0],target_point[0]],[near[1],target_point[1]],c = 'blue', label = 'nearest road', linestyle='--')
    plt.legend()
    plt.show()

还涉及到了一些数据可视化中 matplotlib.pyplot 的部分，好久不做真的会忘。。。

整体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
# from sklearn.neighbors import KDTree
data_list= []
'''
    Time:23/3/16 20点35分
    Auther:Nexus
'''
def read_data_set():
    with open("NE.txt","r") as f :
        for line in f.readlines():
            line = line.strip('\n').split(' ')
            data_list.append(line)

# ax + b + noise     
def encrypt_data(message):
    a = random.uniform(10.0,20.0)
    b = random.uniform(1.1/100000,2.1/100000)
    noise = random.uniform(0,0.000005)
    encrypted = a*message + b + noise
    return encrypted

class Node:
    def __init__(self,point) -> None:
        self.point = tuple(point)
        self.left = None
        self.right = None
class KD_tree:
    def __init__(self,k) -> None:
        self.k = k

    def create_KD_tree(self, new_data, depth):
        if not new_data:
            return None
        # 排序原因 在这个函数中，通过对数据集进行排序，
        # 可以更快地找到中位数并进行坐标轴划分，
        # 从而构建一棵 平衡的 kd-tree。
        mid_index = len(new_data) // 2 # 中位数坐标
        cd = depth % self.k # 对应层数比较
        sorted_new_data = sorted(new_data,key=(lambda p:p[cd]))
        median = new_data[mid_index] # 中位数
        cur_Node = Node(median) # 创建当前结点
        left_children = sorted_new_data[:mid_index]
        right_children = sorted_new_data[mid_index+1:]
        cur_Node.left = self.create_KD_tree(left_children,depth+1)
        cur_Node.right = self.create_KD_tree(right_children,depth+1)
        return cur_Node

    def search(self, tree, new_data):
        self.near_point = None #当前最邻近点
        self.near_val = None #当前最邻近点与目标节点之间的距离

        def dfs(node, depth):
            #递归找叶子结点
            if not node:
                return
            axis = depth % self.k
            if new_data[axis] < node.point[axis]:
                dfs(node.left, depth + 1)
            else:
                dfs(node.right, depth + 1)

            # 比较距离，判断是否更新最邻近点
            dist = self.distance(new_data, node.point)
            if not self.near_val or dist < self.near_val:
                self.near_val = dist
                self.near_point = node.point

            # 向上回退的时候判断是否需要进入另一个子节点寻找
            if abs(new_data[axis] - node.point[axis]) <= self.near_val: 
                if new_data[axis] < node.point[axis]: 
                    dfs(node.right, depth + 1) 
                else:
                    dfs(node.left, depth + 1)
            

        dfs(tree, 0)
        return self.near_point
    def distance(self,point1, point2):
        res = 0
        for i in range(self.k):
            res += (point1[i]-point2[i])**2 
        return res ** 0.5

if __name__ == '__main__':
    read_data_set()
    print("NE数据集如下:")
    print(pd.DataFrame(data_list,
                        columns=['x','y']))
    encrypted_list = []
    for data in data_list :
        data[0] = encrypt_data(float(data[0]))
        data[1] = encrypt_data(float(data[1]))
        # 这里用 float 是因为 data 是列表类型
        # 而加密函数中乘的 a 是 float 类型
        # 因此会报错
        data = tuple(data)
        encrypted_list.append(data)

    print("加密后NE数据集如下:")
    print(pd.DataFrame(encrypted_list,
                        columns=['x','y']))
    
    while 1:
        data_set = encrypted_list[:30]
        target_point = input("请输入查询坐标:").split(',')
        target_point = list(map(float,target_point))
        kd_tree = KD_tree(2)
        tree = kd_tree.create_KD_tree(data_set, 0)
        near = kd_tree.search(tree,target_point)
        print('离{}最近的点为: {}'.format(tuple(target_point),near))
        
        plt.scatter([x[0] for x in data_set],[x[1] for x in data_set],c = 'black', label = 'NE Dataset')
        plt.scatter(target_point[0],target_point[1],c = 'red', label = 'target_point')
        plt.plot([near[0],target_point[0]],[near[1],target_point[1]],c = 'blue', label = 'nearest road', linestyle='--')
        plt.legend()
        plt.show()

👋 sklearn也有 KDtree 的包，不过没调懂 ……

实验结果

输入查询坐标，结果在可视化界面进行验证：

1
2
3
4
# 选取的数据为
# (3,3)
# (5,9)
# (12,4)

实验感想

通过本次实验，我了解并掌握了KD树在数据安全中的应用，也深刻提高了代码能力，认识到代码能力的重要性，最后还通过数据可视化技术进行验证，对可视化技术进行了深入的复习，获益匪浅。

附录-参考文献

郭晶晶, 苗美霞, 王剑锋. 保序加密技术研究与进展. 密码学报. 2018, 5(2): 182-195 https://doi.org/10.13868/j.cnki.jcr.000230

Search and Insertion in K Dimensional tree

-------------本文结束感谢您的阅读-------------
请作者喝一杯蜜雪冰城吧！