Meta Field
0%

复试机考

发表于 更新于 Valine：
本文字数： 30k 阅读时长 ≈ 27 分钟

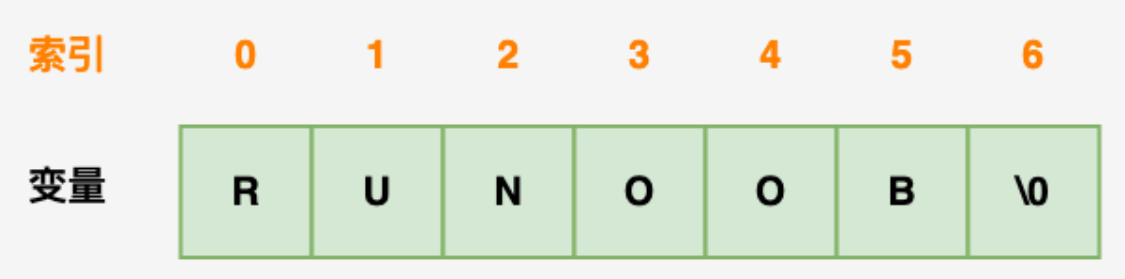
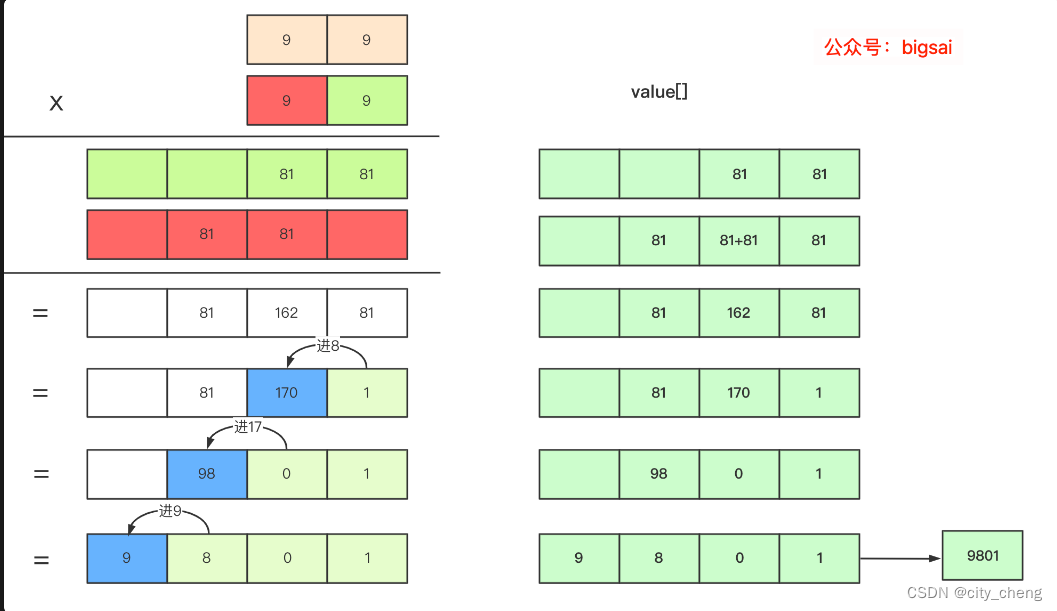
coding

45 skew数

描述

在 skew binary 表示中，第 k 位的值 x[k] 表示 x[k]×(2^(k+1)-1)。每个位上的可能数字是 0 或 1，最后面一个非零位可以是 2，例如，10120(skew) = 1×(2^5-1) + 0×(2^4-1) + 1×(2^3-1) + 2×(2^2-1) + 0×(2^1-1) = 31 + 0 + 7 + 6 + 0 = 44。前十个 skew 数是 0、1、2、10、11、12、20、100、101、以及 102。

输入描述：

输入包括多组数据，每组数据包含一个 skew 数。

输出描述：

对应每一组数据，输出相应的十进制形式。结果不超过 2^31-1。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<bits/stdc++.h>
using namespace std ;
int main(){
    string str ;
    while(getline(cin,str)){
        int sum = 0 ;
        int j = str.size() ;
        for(int i=0;i<str.size();i++){
            sum += (str[i]-'0')*(pow(2,j)-1) ;
            j-- ;
        }
     cout<<sum<<endl ;
    }
    return 0;
}

知识点

①字符串构造

1
char s[] = "RUNOOB"

image-20240229152822292

②循环输入

c++： while(getline(cin,str)) {}

输入流成员函数getline()：从输入流中读取字符，直到遇到指定的分隔符（默认为换行符）或 到达文件结尾。

c：while(scanf("%d",&n) != EOF) {}

EOF：End of File 通常在文本的最后存在此字符表示资料结束，ASCII码中字符是 ctrl+Z，实际上EOF值常为 -1 ，常被用来判断调用一个函数是否成功。

③c++中 string类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
string str		//生成字符串
string s(str)	//生成字符串s为str的复制品
string s(num,ch) //生成num个ch字符的字符串
string s(str, strbegin, strlen) //将字符串str中从下标strbegin开始，保留strlen个字符，其余丢弃
string s(str, stridx) //将字符串str中从下标stridx开始到最后保留，其余丢弃
    
s.size(),s.length():	//返回string对象的字符个数（不包含空字符），效果相同 eg:abc=>length = 3（不用考虑‘0’）
s.max_size():	//返回string对象最多包含的字符数，超出会抛出length_error异常
s.capacity():	//重新分配内存之前，string对象能包含的最大字符数

cin >> s1 ;	//单字符串输入，读入字符串，遇到空格或回车停止
cin >> s2 >> s3 ; //多字符串输入，遇到空格代表当前字符串赋值完成，转到下个字符串赋值
getline(cin,s4); //最终读入字符串中保留空格，如 ”abc de fg“

str[i] str可以作为数组来使用

④string的插入：push_back() 和 insert()

1
2
3
4
5
6
7
8
9
10
string s ;
push_back() // 尾插一个字符
s.push_back('a') ;
s.push_back('b') ;
s.push_back('c') ;
s:abc

insert（pos,char) // 在指定位置pos前插入字符char
s.insert(s1.begin(),'1');
s:1abc

17 n的阶乘

老生长谈了，不过也学到点新东西

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std ;

long int fac(int a){
    if(a==0){ //递归结束条件
        return 1 ;
    }
    else{
        return a*fac(a-1) ;
    }
}

int main()
{
    int n ;
    cin>> n;
    cout<<fac(n) ;
    //printf("%ld",fac(n)) ;
    return 0 ;
}

long int 和 long long以及输出

long int 就是 long，4个字节，32位

longlong是长整型，8个字节，64位

1
2
3
printf("%d",l);	//long
printf("%d",i);	//int
printf("%lld",ll); //longlong 64位输出用这个，来自 牛客网 的提示

37 结构体排序

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
using namespace std ;
struct mouse{
    int weight ;
    string color ;
};
bool cmp(mouse x,mouse y){
    return x.weight > y.weight ; // 从大到小 >
}

int main()
{
    int n ;
    cin >> n ;
    struct mouse m[100] ;
    for(int i=0; i<n; i++){
        cin>>m[i].weight>>m[i].color ;
    }
    sort(m,m+n,cmp) ;
    for(int i=0; i<n; i++){
        cout<<m[i].color<<endl ;
    }
    return 0 ;
}

sort()在结构体中的使用

1.不考虑数据相同

1
2
3
4
5
6
7
8
9
struct node{
	int val ;
	char[10] ;
};
struct node a[100] ;
bool cmp(node x, node y){
	return x.val > y.val ; //从大到小 > ; 从小到大 <
}
sort(a,a+n,cmp) ;

2.考虑数据相同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
struct node{
	int val ;
	int val2;
     char[10];
};
struct node a[100] ;
bool cmp(node x, node y){
	if(x.val < y.val){ //从小到大排序
        return true ;
	}else{
        if(x.val == y.val){
            if(x.val2<y.val2){
                return true ;
            }
        }
    }
    return false ;
}
sort(a,a+n,cmp) ;

3.cmp自定义

比如有数大小升序降序排列，还有位数顺序降序排列，比如华东师大22保研第一题：

1
2
3
4
5
6
7
8
9
bool cmp(int a, int b){
    int la = to_string(a).size() ;
    int lb = to_string(b).size() ;
    if(a<0) la-- ;
    if(b<0) lb-- ;
    if(la!=lb) return la>lb ;
    return  a<b ;
}
sort(v.begin(),v.end(),cmp);

52 位操作

位运算相关还不是很熟练啊

描述

给出两个不大于65535的非负整数，判断其中一个的16位二进制表示形式，是否能由另一个的16位二进制表示形式经过循环左移若干位而得到。 循环左移和普通左移的区别在于：最左边的那一位经过循环左移一位后就会被移到最右边去。比如： 1011 0000 0000 0001 经过循环左移一位后，变成 0110 0000 0000 0011, 若是循环左移2位，则变成 1100 0000 0000 0110

输入描述：

每行有两个不大于65535的非负整数

输出描述：

对于每一行的两个整数，输出一行，内容为YES或NO

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
using namespace std;

int main() 
{
    unsigned short a, b;//非负整数 用无符号即可 如果是int会有最高位符号位
    while (cin >> a >> b)
    {
        bool flag = false;
        for (int i = 0; i < 16; ++i)
        {
            if (b >> 15 & 1) //最高位是1 b右移15位和1相与，如果是1说明最高位是1
                b = b << 1 | 1; //此时左移1位，并将末尾填1补充
            else //最高位是0
                b = b << 1; //直接左移1位，不用补充1
            if (a == b)
            {
                flag = true;
                break;
            }
        }
        flag ? puts("YES") : puts("NO");
    }
}

①无符号数

如果用有符号数，第一位是符号位，直接这么移动会导致真值与题意不符。

②最后的判断比较精简

一般会想到用if，但本题解用了三元运算符，更简洁

101 Powerful Calculator

一个题考了大数的加，减，乘然后说：这是入门题。SJTU牛逼

大数加减乘本质是模拟，用计算机来模拟纸笔运算过程。大数除法不太一样，它是转换成特殊的加减法运算。在Java中我们可以使用一个大数类(BigInteger等)很容易解决大数的各种运算，但如果遇到面试官他肯定会让你手写的。

大数加法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
string Add(string a, string b){
	string ans = "" ;
	int len = max(a.size(),b.size()) ; // 两数对齐
	while(a.size() < length) a = "0" + a ; //头部补0
	while(b.size() < length) b = "0" + b ; //补0
	int carry = 0 ; //进位
	int temp ; //中间变量
	// 模拟从最后一位到第一位按位相加
	for(int i=len-1; i>=0; i--){
		temp = a[i]-'0' + b[i]-'0' + carry ;
		if(temp > 9){
			carry = 1 ;
			ans += temp - 10 + '0' ;
		}else{
			carry = 0 ;
			ans += temp + '0' ;
		}
	}
	if(carry == 1) a += "1" ;
	reverse(ans.begin(),ans.end()) ; //最后逆置一下
	return string ;
}

大数减法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/*先判断被减数和减数的长度，若为被减数长则结果为正，否则为负。若而这长度相等，
则判断哪个数大，不然最后再处理负号会很麻烦。
其他的思想就和加法很像了，有个借位的变量，从低位开始*/
string Sub(string a, string b){
    bool flag ;//true 正 false 负
    int len1 = a.size() ;
    int len2 = b.size() ;
    int len ;
    if(len1>len2){
        flag = true ;
        len = len1 ;
    }else if(len1<len2){
        flag = false ;
        len = len2 ;
        swap(a,b) ;
    }else{//长度相等判断哪个数大
        int i ;
        for(i=0; i<len1; i++){
            if(a[i]>b[i]){// a>b
                flag = true ;
                len = len1 ;
                break ;
            }else if(a[i]<b[i]){
                flag = false ;
                len = len2 ;
                swap(a,b) ; //如果a<b要记得交换 a b
                break ;
            }
        }
        if(i==len1) return "0" ;//此时俩数一样
    }
    while(a.size()<len) a = "0" + a ;
    while(b.size()<len) b = "0" + b ;
    int borrow = 0 ;int temp ;
    string ans = "" ;
    for(int i=len-1;i>=0;i--){
     	temp = (a[i]-'0') - (b[i]-'0') - borrow ;
        if(temp < 0){
         	borrow = 1 ;
            temp += 10 ;
            ans += temp + '0' ;
	    }else{
            borrow = 0 ;
            ans += temp + '0' ;
        }
	}
    int j = ans.size() - 1 ;
    while(ans[j]=='0') j-- ;
    ans = ans.substr(0,j+1) ;
    reverse(ans.begin(),ans.end()) ;
    if(flag) return ans ;
    else return "-" + ans ;
}

大数乘法

在这里插入图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
string multiString(string a,string b){//
    int ans[MAX] = {0};
    reverse(a.begin(),a.end());
    reverse(b.begin(),b.end());//为了方便先颠倒过来
    int length1 = a.size();
    int length2 = b.size();
    int temp;
    for (int i = 0; i < length1; ++i) {//num3低字节存储地位，所以num3记得颠倒
        for (int j = 0; j < length2; ++j) {
            temp = (a[i]-'0')*(b[j]-'0');
            ans[i+j] += temp;
        }
    }
    for (int i = 0; i < MAX; ++i) {
        if (ans[i] > 9){
            temp = (ans[i] - ans[i]%10)/10;//得到进位值，比如191==>19,19/10 = 1
            ans[i] = ans[i]%10;
            ans[i+1] += temp;
        }
    }
    int i = MAX-1;
    while (ans[i] == 0)
        --i;//消除前导0,i+1为长度
    string str = "";
    for (int j = 0; j < i+1; ++j) {
        str += ans[j]+'0';
    }
    reverse(str.begin(),str.end());
    return str;
}

115 后缀字串排序

对于一个字符串，将其后缀子串进行排序，例如grain 其子串有： grain rain ain in n 然后对各子串按字典顺序排序，即： ain,grain,in,n,rain

简单题直接上代码

1
2
3
4
5
6
7
8
9
10
11
12
#include<bits/stdc++.h>
using namespace std ;
int main(){
    string s ;
    cin >> s ;
    int len = s.size() ;
    vector<string> strs(len) ;
    for(int i=0; i<len; i++)    strs[i] = s.substr(i,len);
    sort(strs.begin(),strs.end());
    for(int i=0; i<len; i++)    cout<<strs[i]<<endl ;
    return 0 ;
}

68 子串出现次数

补充知识点：C++ map

map完成任何基本类型到任何基本类型的映射，int a[]事实上就是定义一个 int 到 int 的映射。

map提供一对一的数据处理，key-value键值对，其类型可以自己定义，第一个称为关键字，第二个为关键字的值。map内部自动排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//初始化
map<string,int> m ;
//下标访问容器内元素
maps['c'] = 5 ;
//顺序迭代器访问容器内元素
for(map<char,int>::iterator it = m.begin();it!=m.end();it++)
    cout<<it->first<<" "<<it->second<<endl ;
//逆序迭代器访问容器内元素
for(map<char,int>::iterator it = m.rbegin(); it!=m.rend();it++)
    cout<<it->first<<" "<<it->second<<endl ;
//first => key ; second => value

//insert pair<...>(...) 插入
m.insert(pair<string,int>("ttt",111)) ;
//数组方式插入
m['d'] = 16 ;

//清空
m.clear() ;
//删除元素
m.erase() ;
int n = m.erase("111") ;//如果删除了返回1，否则返回0
//删除整个map
m.erase(m.begin(),m.end());
//获取map长度
int len = m.size() ;

//m[num] 默认值是0

题目与代码

给出一个01字符串（长度不超过100），求其每一个子串出现的次数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<bits/stdc++>h>
using namespace std ;
int main(){
	map<string,int>myMap ;
	string str ;
    cin>>str ;
    for(int i=0; i<str.size; i++){
        for(int j=i; j<str.size(); j++){
			map[str.substr(i,j-i+1)]++ ;
        }
	}
    for(map<string,int>::iterator it = myMap.begin(); it!=myMap.end(); it++){
		if(it->second>1){
			cout<<it->first<<" "<<it->second<<endl ;
        }
    }
	return 0 ;
}

存树&图

树的本质是无向无环图，所以存树和存图可以说没有本质区别。

存图有两种方式：1.给出所有的边； 2.给出邻接矩阵

1.给出所有边

给定点的个数和边的个数，通常记作 和 ，接着给出 行，每行两个整数 代表第 条边所连接的两个点。如果这张图带权，则每行就是三个整数，第三个整数是权值。以这一题为例：P1224 携程-2023.04.15-春招-第三题-魔法之树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 图的存储:开一个可变长二维数组，这1001个数组中的每个元素都是一个不定长数组 vector<int>
//塔子哥版本用的是 *二位变长数组* ，OIwiki用的是结构体，都行
vector<int> e[1001] ;
//注意与 vector<int> e 的区别，这是定义了 一个 不定长数组
int n ; cin >> n ;
for(int i = 1; i<n; i++){ // i<n 是因为树的n个点有n-1个边
    int x, y ;
    cin >> x >> y ;
    e[x].push_back(y) ;
    e[y].push_back(x) ;
    // 由于你无法确认x,y之间谁是父亲节点，所以需要存双向边,
    // 在dfs的过程中防止返祖即可(返祖会引发死递归!)。
    // PS:在有一些题目里，他会明确规定谁是父亲,这种情况下就不用存双向边，
    // 且在dfs的过程中也不用担心返祖的问题.
}

本例题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std ;
const int N = 1010 ;
vector<int> e[N] ;
int w[N] ; //int范围是10位数，此处远超，所以要用LL
int cnt = 0; 
typedef long long LL ;
LL n, l ,r ;

void dfs(int u, int fa, int pre){
    int cur = pre*2 + w[u] ;
    if(cur > r) return ;
    else if(cur >= l) cnt++ ;
    for(auto &x : e[u]){
        if(x==fa) continue ;
        dfs(x,u,cur) ;
    }
}

int main(){
    cin >> n >> l >> r ;
    string s ;
    cin >> s ;
    for(int i=1; i<=n; i++) w[i] = s[i-1]-'0' ;
    for(int i=1; i<n; i++){
        int u , v ;
        cin >> u >> v ;
        e[u].push_back(v) ;
        e[v].push_back(u) ;
    }
    for(int i=1; i<=n; i++) dfs(i,-1,0) ;
    cout<<cnt<<endl ;
    return 0 ;
}

补充知识点：

①auto

auto已经失去了最开始他本身的含义，C++11委员会现在对auto的定义：auto在声明变量时根据初始化表达式自动推断该变量的类型；声明函数时函数返回值的占位符。

呃呃什么是占位符？好好好，又有一个没见过的

占位符就是先占住一个固定的位置，等着你再往里面添加内容的符号，广泛用于计算机中各类文档的编辑。

格式占位符(%)是在C/C++语言中格式输入函数，如 scanf、printf 等函数中使用。其意义就是起到格式占位的意思，表示在该位置有输入或者输出。

下面回到auto：

1
2
3
4
5
6
auto i = 5 ;	// 推断为int
auto str = "hello auto";	// 推断为const char*
auto sum(int a1, int a2)->int	// 返回类型后置,auto为返回值占位符
{
	return a1 + a2 ;
}

编译器对auto的推断是从左往右的，比如这句代码就会出错：

1
2
auto x = 1, y = 4.2 ;
// x是int，y是double

auto使用表达能力更强的类型，比如这句代码：

1
auto x = true ? 1 : 4.2 ; // x会被推断为double类型

②dfs以及本题的逻辑

dfs最基本模板

1
2
3
4
5
6
7
void dfs(int u){//输入结点
	if(vis[u]) return ;//如果vis过了就回退
	vis[u] = true ;
	for(int i=1; i<=m; i++){
		if(e[i].u==u) dfs(e[i].v) ;//递归访问下一个结点
	}
}

然后看这道题dfs怎么写：

1
2
3
4
5
6
7
8
9
void dfs(int u, int fa, int pre){
    int cur = pre*2 + w[u] ;
    if(cur > r) return ;
    else if(cur >= l) cnt++ ;
    for(auto &x : e[u]){
        if(x==fa) continue ;
        dfs(x,u,cur) ;
    }
}

首先想输入有什么，有当前结点u，考虑到回退要有父节点fa，还有在该结点之前的路径和pre，所以

1
void dfs(int u, int fa, int pre){}

然后我想以递归方式来写这个函数，那么就要考虑递归退出的条件，题目要求范围在之间，所以当前的路径和cur加到大于r后就可以退出，所以

1
2
3
4
5
6
void dfs(int u, int fa, int pre){
	int cur = pre*2 + w[u] ; //*2+w[u]相当于2进制数左移1位再补权值做末位,如此往复得到最终二进制数
	if(cur > r) return ;
	else if(cur >=l) cnt++ ; //表示找到一种路径
	......
}

到这里只是对其中一个点的dfs，我们要对所有点dfs，所以要写一个循环

1
2
3
4
5
6
7
8
9
10
void dfs(int u, int fa, int pre){
	int cur = pre*2 + w[u] ;
	if(cur > r) return ;
	else if(cur >=l) cnt++ ; //表示找到一种路径
	for(auto &x:e[u]){ //此处我们并不知道u连着多少个点（e[u]数组有多少个元素我们是不知道的），所以可以用auto
		if(x==fa) continue ; //continue：跳过当前循环中的代码，强迫开始下一次循环
		//如果x是e[u]的父节点，那就没必要往父节点那里dfs，强制进行下一轮
		dfs(x,u,cur) ;//x不是u的父节点，那就是u的子节点，所以下面就要visit x，把x的父节点u放到fa的位置，cur放到pre
	} 
}

③int范围与何时使用long long

我们平时使用的电脑是64位，根据计组，范围是 ，十进制是2开头的10位数，本题给的范围是 ，显然超过了int范围，所以我们要用 long long。

1
2
typedef long long LL ;
LL n, l, r ;

④OI wiki上的图的存储，用了结构体

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//先定义边 Edge
struct Edge{
	int u, v ;
};
vector<Edge> e ;
vector<bool> vis ;

//假设有n个结点和m条边
bool find_edge(int u, int v){
    for(int i=1; i<=m; i++){
        if(e[i].u==u && e[i].v==v) return true ;        
    }
	return false ;
}

int main(){
	int n , m ;
	cin>>n>>m;
	vis.resize(n+1,false) ; 
	e.resize(m+1) ;
    for(int i=1; i<=m; i++) cin >> e[i].u >> e[i].v ;
    return 0 ;
}

继续补充： resize()

1
2
void resize (size_type n);
void resize (size_type n, const value_type& val);

改变容器大小，使得其包含n个元素，常见有3种用法：

1.如果n小于当前的容器大小，那么则保留容器的前n个元素，去除超过的部分。

2.如果n大于当前的容器大小，则通过在容器结尾插入适合数量的元素使得整个容器大小达到n。且如果给出val，插入的新元素全为val。

3.如果n大于当前容器的容量(capacity)时，则会自动重新分配一个存储空间。

2.给出邻接矩阵

给定点的个数 , 接下来行，直接给出邻接矩阵 , 代表之间有一条边， 代表没有边，直接用二维数组表示

3.树的读入

（树存储等同于图存储）

读入：根据树的无向无环性质，有这样一种方式：给出父亲节点数组

给出 个正整数 $pi表示第i个节点的父亲，其中规定1$ 号节点是根节点

例题 P1141 美团-2023.04.01-第五题-染色の树

加减乘除 — Switch语句复习

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<bits/stdc++.h>
typedef long long LL ;
using namespace std;
void j(LL a){
    int sum = 1 ;
    for(int i=1; i<=a; i++) sum *= i ;
    cout<<sum<<endl ;
}

void f(LL a, char s, LL b){
    switch(s){
        case '+':
                cout<<a+b<<endl ; break ;
        case '-':
                cout<<a-b<<endl ; break ;
        case '*':
                cout<<a*b<<endl ; break ;
        case '/':
                if(b==0){
                    cout<<"error"<<endl ;break ;
                }else cout<<a/b<<endl ;break ;
        case '%':
                if(b==0){
                    cout<<"error"<<endl ;break ;
                } else cout<<a%b<<endl ;break ;
    }
}

int main(){
    LL a, b ;
    char s ;
    while(cin>>a>>s){
        if(s=='!') j(a) ;
        else{
            cin>>b ;
            f(a,s,b) ;
        }

    }
    return 0 ;
}

ASCII码基础相关

65-90 ：大写英文字母；97-122：小写英文字母

本质是简单的凯撒密码

1
2
3
4
 for(int i=0; i<s.size();i++){
       if('A'<=s[i]&&s[i]<='Z')
           s[i] = (s[i] -'A'- 5 + 26)%26 + 'A' ;
}

s[i]-‘A’：将字符转换为相对于大写字母’A’的偏移量； -5 是题目要求；+26是处理负偏移；%26是保证结果在0-25之间，再加’A’得到偏移后的字符的ASCII码值。

C++ 字符串匹配(s.find()函数相关)

string的find函数：

1.正向查找 find()

​ 1) s.find(str);

​ 2) s.find(str, pos);

​ 3) s.find_first_of(str); 和 s.find_last_of(str);

​ 4)例题：查找目标字符串在字符串中出现总次数

2.逆向查找 rfind()

1.find

1.1 s.find(str)

字符串从左往右查找，最后返回字母在母串中的下标位置

如果没找到，那么会返回一个特别的标记npos，一般写作string::npos 。

1
2
3
4
5
6
7
8
9
10
#include<bits/stdc++.h>
using namespace std ;
int main(){
	string s, c ;
	s = "apple" ;
	c = "l" ;
	cout<<s.find(c)<<endl ;
	return 0 ;
}
//输出结果：3

1.2 s.find(str,pos)

寻找从 pos 开始匹配str的第一个位置

1
2
3
4
5
6
7
8
9
10
#include<bits/stdc++.h>
using namespace std ;
int main(){
	string s, c ;
	s = "lbhfuaerfvfkyfwr" ;
	c = "f" ;
	cout<<s.find(c,2)<<endl ;
	return 0 ;
}
//输出结果：只有 8

1.3 s.find_first_of(str) s.find_last_of(str)

找到目标字符在字符串中第一次出现和最后一次出现的位置

1
2
3
4
5
6
7
8
9
10
11
12
#include<bits/stdc++.h>
using namespace std ;
int main(){
	string s, c ;
	s = "lbhfuaerfvfkyfwr" ;
	c = "f" ;
	cout<<s.find_first_of(c)<<endl ;
	cout<<s.find_last_of(c)<<endl ;
	return 0 ;
}
//3
//13

1.4 查找目标字符串在字符串出现的总次数

法1：核心代码 s.find(c,index)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<bits/stdc++.h>
using namespace std ;
int main(){
	string s,c ;
	while(cin>>s>>c){
        int index = 0 ;
        int sum = 0 ;
        while((index=s.find(c,index))!=string::npos){
			index++ ; sum++ ;
        }
        cout<<sum ;
    }
	return 0 ;
}

法2：substr(i,length) 思路是从a中不断截取b长度的子串

1
2
3
4
5
6
7
8
9
10
11
12
#include<bits/stdc++.h>
using namespace std ;
int main(){
	string s,c ;
	while(cin>>s>>c){
		int count = 0 ;
         for(int i=0; i<s.size(); i++){
			if(a.substr(i,b.size()) == b) count++ ;
		}
    }
	return 0 ;
}

2.rfind()

1
2
3
string s = "apple";
cout << s.rfind("l") << endl;
//输出 3

KY93 WERTYU 键盘字符串映射

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//C++中的反斜杠是转义字符，所以在制作keymap时候
//要在反斜杠前再填一个反斜杠
//没有想到要用map欸，奇怪的知识点应用又增加了
//好好好好好
#include<bits/stdc++.h>
using namespace std;
int main(){
    string str, res, tmp ;
    map<char,char> keymap ;
    res = "`1234567890-=QWERTYUIOP[]\\ASDFGHJKL;'ZXCVBNM,./" ;
    char ch = ' '; //空格要特殊处理,即自己映射自己
    for(int i=1; i<res.size(); i++)
        keymap[res[i]] = res[i-1] ;
    keymap[ch] = ch ;
    while(getline(cin,str)){
        tmp = str ;
        for(int j=0; j<str.size(); j++)
            tmp[j] = keymap[str[j]] ;
        cout<<tmp ;
        if(cin.get() == '\n') break ;
    }
    cout<<endl ;
    return 0 ;
}

补充：

1.C++中转义字符

反斜杠表示字符串时候前面要再加一个反斜杠

2.涉及到映射关系时候要想map

比如本题就是字符和字符之间的映射，我们就可以定义

1
map<char,char> keymap ;

然后通过循环将字符依次映射到key

c++中的栈、堆

栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//定义
stack<type> name ;
//常用方法
s.empty();         //如果栈为空则返回true, 否则返回false;
s.size();          //返回栈中元素的个数
s.top();           //返回栈顶元素, 但不删除该元素
s.pop();           //弹出栈顶元素, 但不返回其值
s.push();          //将元素压入栈顶

//代码示例
#include<bits/stdc++.h>
using namespace std ;
int main(){
	stack<int> s ; //栈初始化
	for(int i=0; i<10; i++) s.push(i) ; //压栈操作 s.push(val) ;
	cout<<s.size()<<endl ; //返回栈中 *元素个数*
	while(!s.empty()){
		cout<<s.top()<<" " ; 
		s.pop() ;
	}
	return 0 ;
}

栈例题-xdoj74括号匹配

（1）利用栈先进后出的特点，当遇到左括号”[“,”{“,””(“时，直接入栈。

（2）当遇到右括号”)”,”}”,”]”时，如果此时空的，那么成对的括号一定不能进行匹配，直接返回false即可。

（3）可以出栈的情况，当栈顶的左括号与当前的右括号匹配时，出栈。

（4）遍历过程中出现的其他情况都是错误的。比如栈顶为左括号，当前遍历到也是左括号。

（5）当遍历完成时，如果栈不空，说明还有未进行匹配的左括号，也就意味括号匹配失败，直接返回false即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
#include <stack>
using namespace std;

bool isValid(string s) {
    stack<char> st;
    for (auto x : s) {
        if (x == '[' || x == '(' || x == '{')
            st.push(x);
        else if (st.empty())
            return false; 
        else if ( (st.top() == '(' && x == ')') || (st.top () == '[' && x == ']') || (st.top() == '{' && x == '}') )
            st.pop();
        else
            return false;
    }
    return st.empty();
}


int main() {
    string s;
    cin >> s;
    if(isValid(s)) cout<<"yes" ;
    else cout<<"no" ;
    return 0 ;
}

动态规划基础

对于一个能用动态规划解决的问题，一般采用如下思路解决：

  1. 将原问题划分为若干 阶段，每个阶段对应若干个子问题，提取这些子问题的特征（称之为 状态）；
  2. 寻找每一个状态的可能 决策，或者说是各状态间的相互转移方式（用数学的语言描述就是 状态转移方程）。
  3. 按顺序求解每一个阶段的问题。

例1 最长公共子序列

注：子序列与子串区别：

子序列可以不连续，子串必须连续

设 表示只考虑 A 的前 个元素， 的前 个元素时的最长公共子序列的长度，求这时的最长公共子序列的长度就是 子问题。 就是我们所说的 状态，则 是最终要达到的状态，即为所求结果。

对于每个 存在三种决策：

​ 如果 则可将它接到公共子序列末尾

​ 其余是跳过 和

求解动态规划要牢记三个点：

①base case；②状态转移方程；③自下而上

核心代码

1
2
3
4
5
6
7
8
9
10
vector<vector<int> > dp(len1+1,vector<int>(len2+1,0))
//创建名为dp的二维向量,len1+1行，len2+1列，初始值为0
for(int i=1; i<=len1; i++){
    for(int j=1; j<=len2; j++){
        //i,j从1开始遍历，而字符串下标从0开始
        if(s1[i-1]==s2[j-1]) dp[i][j] = dp[i-1][j-1] + 1 ;
        else dp[i][j] = max(dp[i-1][j],dp[i][j-1]) ;
    }
}
//dp[len1][len2]表示最终结果

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<bits/stdc++.h>
using namespace std ;
int main(){
    string s1, s2 ;
    cin >> s1 >> s2 ;
    int l1 = s1.size() ;
    int l2 = s2.size() ;
    if(l1>l2) swap(s1,s2) ;
    vector<vector<int> > dp (l1+1,vector<int>(l2+1,0)) ;
    for(int i=1; i<=l1; i++){
        for(int j=1; j<=l2; j++){
            if(s1[i-1]==s2[j-1]) dp[i][j] = dp[i-1][j-1] + 1 ;
            else dp[i][j] = max(dp[i-1][j],dp[i][j-1]) ;
        }
    }
    cout<<dp[l1][l2] ;
    return 0 ;
}

例2 棋盘游戏

描述

有一个6*6的棋盘，每个棋盘上都有一个数值，现在又一个起始位置和终止位置，请找出一个从起始位置到终止位置代价最小的路径： 1、只能沿上下左右四个方向移动 2、总代价是每走一步的代价之和 3、每步（从a,b到c,d）的代价是c,d上的值与其在a,b上的状态的乘积 4、初始状态为1 每走一步，状态按如下公式变化：（走这步的代价%4）+1。

输入描述：

每组数据一开始为6*6的矩阵，矩阵的值为大于等于1小于等于10的值，然后四个整数表示起始坐标和终止坐标。

输出描述：

输出 最小 代价。

考点：动态规划，图（深搜）

1
2
3
4
5
6
7
8
9
10
11
12
13
int main(){
    for(int i=0; i<6; i++){
        for(int j=0; j<6; j++){
            cin>>matrix[i][j] ;
        }
    }
    int x, y, x2, y2, status = 1 ;
    cin>>x>>y>>x2>>y2 ;
    memset(visited,0,sizeof(visited)) ; //重置visited矩阵
    dfs(x,y,x2,y2,status,0) ; //核心代码，深搜
    cout<<ans ;
    return 0 ;
}

核心思路：深搜与前置条件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#define INF 0x3f3f3f3f 
//常用的常数，要记住
//定义无穷大是因为要初始化代价，然后不断找小值
int ans = INF, tmp ; //tmp是记录总代价的临时变量
int a[] = {1,-1,0,0} ; //定义向上向下
int b[] = {0,0,-1,1} ; //定义向左向右
int matrix[6][6] ; //定义棋盘
int visited[6][6]; //定义遍历矩阵

void dfs(int x, int y, int x2, int y2, int status, int tmp){
    if(x==x2 && y==y2) ans = min(ans, tmp) ; //递归结束条件，到达终点后比较当前tmp给和已有ans取最小值
    else{
        visited[x][y] = 1 ;
        for(int i=0; i<4; i++){//依次计算上下左右的操作
            int newx = x + a[i] ; //根据上下左右操作得到新的x坐标值
            int newy = y + b[i] ; //根据上下左右操作得到新的y坐标值
            if(newx>5 || newx<0 || newy>5 || newy<0 || visited[newx][newy]) continue ; //如果越界则跳过此轮循环直接continue到下一轮
            int cost = matrix[newx][newy] * status ; //计算新增的代价
            int newstatus = (cost % 4) + 1 ; //由题更新状态
            dfs(newx,newy,x2,y2,newstatus,tmp+cost);//继续递归
        }
    }
    visited[x][y] = 0 ;//重置环境
}

完整AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f

using namespace std;
int ans = INF, tmp ;
int a[] = {1,-1,0,0} ;
int b[] = {0,0,-1,1} ;
int matrix [6][6] ;
int visited[6][6] ;

void dfs(int x, int y, int x2, int y2, int status, int tmp){
    if(x==x2 && y==y2) ans = min(ans, tmp) ;
    else{
        visited[x][y] = 1 ;
        for(int i=0; i<4; i++){
            int newx = x + a[i] ;
            int newy = y + b[i] ;
            if(newx > 5 || newx<0 || newy > 5 || newy < 0 || visited[newx][newy])
                continue ;
            int cost = matrix[newx][newy] * status ;
            int newstatus = (cost % 4) + 1 ;
            dfs(newx,newy, x2, y2, newstatus, tmp + cost) ;
        }
    }
    visited[x][y] = 0 ; //重置环境
}

int main(){
    for(int i=0; i<6; i++){
        for(int j=0; j<6; j++){
            cin>>matrix[i][j] ;
        }
    }
    int x, y, x2, y2, status = 1 ;
    cin>>x>>y>>x2>>y2 ;
    memset(visited,0,sizeof(visited)) ;
    dfs(x,y,x2,y2,status,0) ;
    cout<<ans ;
    return 0 ;
}

并查集

初始化

1
2
3
4
5
6
7
8
9
10
11
int fa[MAXN] ;
void init(int n){
	for(int i=1; i<=n; i++) fa[i] = i ;
}

void init(int n){
    for(int i=1; i<=n; i++){
      fa[i] = i ;
      height[i] = 1 ;//也可以是0,这里不要用rank，因为rank是C++ 关键字
    } 
}

补充：C++ rank方法

首先，按秩排列不要用rank了

下面是一点补充：rank用于查找类型的等级，要有头文件 #include<type_traits>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// C++ program to illustrate std::rank 
#include <bits/stdc++.h> 
#include <type_traits> 
using namespace std; 
  
// Driver Code 
int main() 
{ 
  
    cout << "rank of following type:"
         << endl; 
    cout << "int:"
         << rank<int>::value 
         << endl; 
  
    cout << "int[]:"
         << rank<int[]>::value 
         << endl; 
  
    cout << "int[][10]:"
         << rank<int[][10]>::value 
         << endl; 
  
    cout << "int[10][10]:"
         << rank<int[10][10]>::value 
         << endl; 
  
    return 0; 
}

结果：

1
2
3
4
5
rank of following type:
int:0
int[]:1
int[][10]:2
int[10][10]:2

查询

返回节点x的根节点

1
2
3
4
int find(int x){
	if(fa[x]==x) return x ;
	else return find(fa[x]) ;
}

路径压缩

img

1
2
3
int find(int x){
	return fa[x]==x ? x : (fa[x] = find(fa[x])) ;
}

合并

将一颗树的根节点连到另一棵树根节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void Union(int i, int j){
	fa[find(i)] = find(j) ; //找到两个集合的代表元素find(i,j)，再将前者的父节点设为后者
}

void Union(int i, int j){
    int x = find(i), y = find(j) ;
    if(x!=y){
        if(height[x]<height[y]) fa[x] = y ;
        else if(height[x]>height[y]) fa[y] = x ;
        else{
            fa[x] = y ;
            height[y]++ ;
        }
    }
}

例题1 畅通工程

描述

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？

输入描述：

测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。

注意:两个城市之间可以有多条道路相通,也就是说 3 3 1 2 1 2 2 1 这种输入也是合法的 当N为0时，输入结束，该用例不被处理。

输出描述：

对每个测试用例，在1行里输出最少还需要建设的道路数目。

考点：图，并查集（特别是题目中 “最少” 二字，暗示在 Union 操作中要按 秩 合并，因为按秩合并的本质是 把简单的树往复杂的树上移动

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<bits/stdc++.h>
#define MAXN 10005
using namespace std ;
int fa[MAXN] ;
int height[MAXN] ;

void init(int n){
	for(int i=1; i<=n; i++){
		fa[i] = i ;
         height[i] = 0 ;
    }     
}

int find(int x){
    return fa[x]==x ? x : (fa[x] = find(fa[x])) ;
}

void Union(int x, int y){
    x = find(x) ;
    y = find(y) ;
    if(x!=y){
        if(height[x]>height[y]) fa[y] = x ;
        else if(height[x]<height[y]) fa[x] = y ;
        else {
            fa[x] = y ;
            height[y]++ ;
        }
    }
}

int main(){
    int n, m ;
    while(cin>>n>>m){
        if(n==0) break ;
        init(n) ;
        while(m--){//合并一次消耗一条边
			int x, y ;
              cin>>x>>y ;
			Union(x,y);
        }
        int ans = -1 ;
        //如果初始时候全联通了，那就只有一个根节点，ans++为0，不用添加道路
        //如果是两个集合，说明还要有1条路连接，有两个根节点的父亲为自己，answer++操作两次，answer=1。以此类推
        for(int i=1; i<=n; i++){
            if(find(i)==i) ans++ ;
        }
        cout<<ans ;
    }
    return 0 ;
}

例题2 畅通工程升级版

描述

某省调查乡村交通状况，得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可），并要求铺设的公路总长度为最小。请计算最小的公路总长度。

输入描述：

测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 )；随后的N(N-1)/2行对应村庄间的距离，每行给出一对正整数，分别是两个村庄的编号，以及此两村庄间的距离。为简单起见，村庄从1到N编号。 当N为0时，输入结束，该用例不被处理。

输出描述：

对每个测试用例，在1行里输出最小的公路总长度。

示例

输入：

1
2
3
4
5
6
7
8
9
10
11
12
3
1 2 1
1 3 2
2 3 4
4
1 2 1
1 3 4
1 4 1
2 3 3
2 4 2
3 4 5
0

输出：

1
2
3
5

考点：图数据结构存储，并查集，最小生成树Kruskal

题目输入有起点终点和权值，所以我们用结构体更好一些

1
2
3
4
5
6
7
#define MAXN 1005
struct Edge{
	int from ;
	int to ;
	int length ; 
};
Edeg edge[MAXN][MAXN] ;

并查集不用多说直接上模板

关键是Kruskal算法：

①初始化图

②给所有边按照权值大小排序

③遍历所有边计算所铺路的长度

④return 结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
bool cmp(Edge x, Edge y){
    return x.length < y.length ;
}

int Kruskal(int n, int edgeNum){
	Init(n) ;
	sort(edge,edge+edgeNum,cmp) ;
	int sum = 0 ;
	for(int i=0; i<edgeNum; i++){
        Edge cur = edge[i] ;
        if(find(cur.from)!=find(cur.to)){
            Union(cur.from,cur.to) ;
            ans += cur.length ;
        }
    }
    return ans ;
}

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<bits/stdc++.h>
#define MAXN 1005
using namespace std ;
struct Edge{
	int from ;
	int to ;
	int length ;
};
Edge edge[MAXN*MAXN] ;
int fa[MAXN] ;
int height[MAXN] ;

void Init(int n){
    for(int i=1; i<=n; i++){
        fa[i] = i ;
        height[i] = i ;
    }
    return ;
}

int find(int x){
    return fa[x]==x? x : fa[x] = find(fa[x]) ;
}

void Union(int x, int y){
    x = find(x) ; y = find(y) ;
    if(x!=y){
        if(height[x]>height[y]) fa[y] = x ;
        else if(height[x]<height[y]) fa[x] = y ;
        else{
            fa[x] = y ;
            height[y]++ ;
        }
    }
    return ;
}

bool cmp(Edge x, Edge y){
    return x.length < y.length ;
}

int Kruskal(int n, int edgeNum){
    Init(n) ;
    sort(edge,edge+edgeNum,cmp) ;
    int ans = 0 ;
    for(int i=0;i<edgeNum;i++){
        Edge cur = edge[i] ;
        if(find(cur.from)!=find(cur.to)){
            Union(cur.from,cur.to) ;
            ans += length ;
        }
    }
    return ans ;
}

int main(){
	int n ;
    while(cin>>n){
        if(n==0) break ;
        int edgeNum = n*(n-1)/2 ;
        for(int i=0; i<edgeNum; i++) cin>>edge[i].from>>edge[i].to>>edge[i].length ;
        cout<<Kruskal(n,edgeNum)<<endl ;
    }
	return 0 ;
}

总结：畅通工程基础问的是添加多少条边，而升级版问的是添加的这些边的长度之和。

C++ cin 和 getline

做了这样一道题：KY127 统计字符 ，其实这个题真的很简单，就是被输入摆了一道（原来不知道cin的细节

做题过程中还是一如既往地无脑 while(cin>>s1>>s2) ，核心逻辑都对，但就是结果不对，看了题解发现都用 getline ，就又发现一点新大陆。

cin 会传递并忽略任何前导白色空格字符（空格，制表或换行符）。一旦它接触到第一个非空格字符即开始阅读，当它读取到下一个空白字符时，它将停止读取。比如 cin >> name，可以输入“Mark”或“Twin”，但不能输入“Mark Twin”，即不能输入包含嵌入的空格的字符串。

为了解决这个问题，就用getline ，读取整行，包括前导和嵌入的空格，并将其存储在字符串对象中。

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<bits/stdc++.h>
using namespace  std;
int main(){
    string s1;
    while(getline(cin,s1)){
        if(s1=="#") break ;
        string s2 ;
        getline(cin,s2) ;
        for(int i=0; i<s1.size(); i++){
            int cnt = 0 ;
            for(int j=0; j<s2.size(); j++){
                if(s1[i]==s2[j]) cnt++ ;
            }
            cout<<s1[i]<<" "<<cnt<<endl ;
        }
    }
    return 0 ;
}

KY41 放苹果

描述

把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？（用K表示）5，1，1和1，5，1 是同一种分法。

输入描述：

每行均包含二个整数M和N，以空格分开。1<=M，N<=10。

输出描述：

对输入的每组数据M和N，用一行输出相应的K。

核心思路：动态规划+递归

先考虑特殊情况：M为0时，因为什么也没有，即：有一种放法；N为0时，没有盘子，根本放不了，return 0 ；M>=N时，方法 = 至少空一个盘子 + 每个盘子至少有一个苹果；M<N时，方法 = M个苹果放M个盘子。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<bits/stdc++.h>
using namespace std;

int ways(int m, int n){
    if(m==0) return 1 ;
    if(n==0) return 0 ;
    if(m<n)  return ways(m,m) ;
    else return ways(m,n-1) + ways(m-n,n) ; 
}

int main(){
    int m, n ;
    while(cin>>m>>n){
        cout<<ways(m,n)<<endl ;
    }
    return 0 ;
}

华师第2题

题目:输入转为二进制,交换位,再计算十进制数

这个题目确实简单，但是有一个小细节最开始把我卡住了

那就是 vector()的数组越界访问问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std ;
int main(){
    int x, i ,j ;
    cin>>x>>i>>j ;
    vector<int> b(32,0) ;
    int k = 0 ;
    while(x){
        b[k++] = x%2 ;
        x = x/2 ;
    }
    swap(b[i],b[j]) ;
    int ans = 0 ;
    int l = b.size() ;
    for(int i=0; i<l; i++){
        if(b[i]==0) continue ;
        ans += b[i]*pow(2,i) ;
    } 
     cout<<ans ;
}

合并两个排序的链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
ListNode* Merge(ListNode* head1, ListNode* head2){
	if(head1==NULL) return head2 ;
	if(head2==NULL) return head1 ;
	ListNode* head = new ListNode(0) ;
	ListNode* cur = head ;
    while(head1 && head2){
        if(head1->val<=head2->val){
            cur->next = head1 ;
            head1 = head1->next ;
        }else{
            cur->next = head2 ;
            head2 = head2->next ;
        }
        cur = cur->next ;
    }
    if(head1) cur->next = head1 ;
    if(head2) cur->next = head2 ;
    return head->next ;
}

链表环的入口

法1：哈希表

当时一拿到题目直接想到哈希表，看了题解有用 unordered_set的，就了解一下，知道这东西是个集合就可以了，再就是知道了unordered_map.count(XXX)的应用。

1
2
3
4
5
6
7
8
9
10
ListNode* EntryNodeOfLoop(ListNode* head){
    if(head==NULL) return NULL ;
    while(pHead){
        unordered_map<ListNode*> st ;//当然这里用set也是可以的
        if(st.count(pHead->val)) return pHead ;
        st.insert(pHead);
        pHead = pHead->next ;
    }
    return NULL ;
}

法2：先检测有无环，再计算入口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
ListNode* hasCycle(ListNode* head){
    //快慢指针
    if(head==NULL) return NULL ;
    ListNode* fast = head ;
    ListNode* slow = head ;
    while(fast=NULL && fast->next!=NULL){
        fast = fast->next->next ;
        slow = slow->next ;
        if(fast==slow) return slow ;
    }
    return NULL ;//到末尾则没有环
}

ListNode* EntryNodeOfLoop(ListNode* pHead){
    ListNode* slow = hasCycle(pHead) ;
    if(slow==NULL) return NULL ;
    ListNode* fast = pHead ;
    while(fast!=slow){
        fast = fast->next ;
        slow = slow->next ;
    }
    return slow ;
}

两链表的第一个公共结点

1
2
3
4
5
6
7
8
9
ListNode* FindFirstCommonNode(ListNode* pHead1, ListNode* pHead2){
    ListNode* l1 = pHead1 ;
    ListNode* l2 = pHead2 ;
    while(l1!=l2){
        l1 = (l1==NULL)? pHead2: l1->next;
        l2 = (l2==NULL)? pHead1: l2->next;
    }
    return l1 ;
}

让N1和N2一起遍历，当N1先走完链表1的尽头（为null）的时候，则从链表2的头节点继续遍历，同样，如果N2先走完了链表2的尽头，则从链表1的头节点继续遍历，也就是说，N1和N2都会遍历链表1和链表2。

因为两个指针，同样的速度，走完同样长度（链表1+链表2），不管两条链表有无相同节点，都能够到达同时到达终点。

（N1最后肯定能到达链表2的终点，N2肯定能到达链表1的终点）。

所以，如何得到公共节点：

  • 有公共节点的时候，N1和N2必会相遇，因为长度一样嘛，速度也一定，必会走到相同的地方的，所以当两者相等的时候，则会第一个公共的节点
  • 无公共节点的时候，此时N1和N2则都会走到终点，那么他们此时都是null，所以也算是相等了。

C++ 逆序字符串

1
2
3
string str = "QWEASD" ;
reverse(str.begin(),str.end()) ;
//关键是reverse函数

链表删除重复元素

1
2
3
4
5
6
7
8
9
10
11
12
13
ListNode* deleteDuplicates(ListNode* head) {
        // write code here
        if(head==NULL) return NULL ;
        ListNode* cur = head ;
        while(cur != NULL && cur->next!=NULL){
            if(cur->val==cur->next->val){
                cur->next = cur->next->next ;
            }else{
                cur = cur->next ;
            }
        }
        return head ;
    }

链表奇偶重排

将链表的奇数位节点和偶数位节点分别放在一起，重排后输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
ListNode* oddEvenList(ListNode* head) {
        //如果链表为空，不用重排
        if(head==NULL) return NULL ;
        //even开头指向第二个节点，可能为空
        ListNode* even = head->next ;
        //odd开头指向第一个节点
        ListNode* odd = head ;
        //指向even开头
        ListNode* evenhead = even ;
        while(even!=NULL && even->next!=NULL){
            //odd连接even的后一个，即奇数位
            odd->next = even->next ;
            //odd进入后一个奇数位
            odd = odd->next ;
            //even连接后一个奇数的后一位，即偶数位
            even->next = odd->next ;
            //even进入后一个偶数位
            even = even->next ;
        }
        //even整体接在odd后面
        odd->next = evenhead ;
        return head ;
    }
-------------本文结束感谢您的阅读-------------
请作者喝一杯蜜雪冰城吧！